When I am setting homework or exam questions for my students I always check them first, but when I am actually teaching I often allow my students to invent their own problems. This can be interesting, and sometimes leads us into “uncharted waters”.
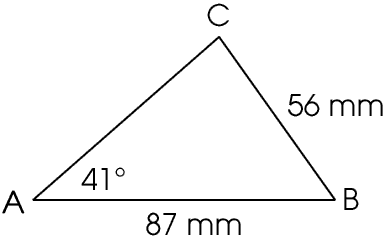
In a lesson on the Sine and Cosine Rules I asked a student to draw a triangle and then measure two sides and one angle. This is her triangle.

So sin C = 1.019
Which is impossible, and if you try sin-1 1.019 on your calculator you will get a maths error. Sadly, at this point some teachers will just say “You must have made a mistake,” and some students may actually believe this. It is not true of course, but in spite of much searching I have been unable to find any explanation in any book or web page which corrects or explains this.
The first and most important thing to do was to reassure my student that she had not made a mistake. Then we checked her calculations. Then we checked her measurements. Then we checked that the sides of her triangle really were straight lines. Finally we measured angle C. It was 85°, and this is the key to understanding what is happening.
We need to look at the graph of sin θ against θ in the Trigonometry and the Sine and Cosine Rules Page. We can see that near θ = 90° the curve is very flat, meaning that a very tiny change in the value of sin θ produces a far from tiny change in the value of θ. In fact, although sin θ can have any value from 0 to 1, it is more than 0.98 for all values of θ between 80° and 100°. Check this for yourself.
We can also see this graphically. In my student’s triangle angle A is acute and BC is less than AB. AE is AC extended. If we draw an arc with its centre at B, depending on the length of the arc (and of course AB and angle A), it will either cut AE at two places, making two triangles, one with an acute angle at C and one an obtuse angle (sin C less than 1), or make AE a tangent to the arc at C making a right angle at C (sin C = 1), or not cut AE at all (sin C greater than one).
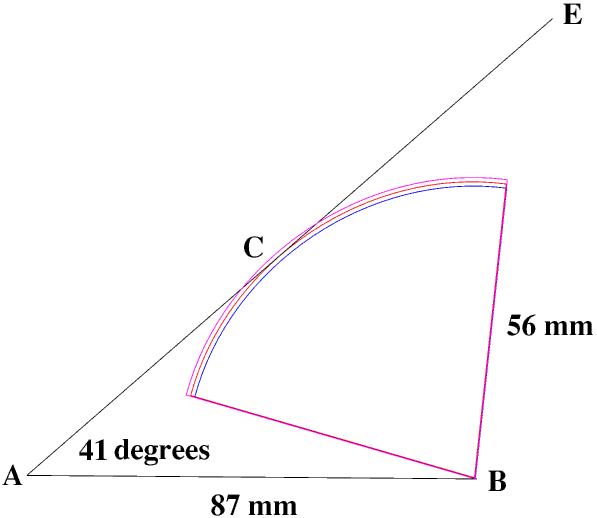
If the angle C is very close to a right angle then the tiniest error in the length of BC (or of course AB or angle A) will make the difference between two triangles, one triangle or no triangle at all.
The lowest value of sin C occurs with the lowest values of A and c and the highest value of a, and the highest value of sin C occurs with the highest values of c and A and the lowest value of a.
If we measure the lengths to the nearest millimetre and angles to the nearest degree then a is in the range 55.5 mm to 56.5 mm, c is in the range 86.5 mm to 87.5 mm and A is in the range 40.5° to 41.5°. So sin C is in the range 0.99429 to 1.04467 so its lowest value is 0.99429 and so to the nearest tenth of a degree C is in the range 83.9° to 96.1°, and our measured value of 85° is within this range.
Summarising all of this, when we are using the Sine Rule to find angles of between 80° and 100°, we need to consider the accuracy of our data with more than ordinary care. For this reason you are unlikely to come across such a problem in an exam at normal school leaving age unless the Paper has not been checked properly. But you might come across it if you are just making up a triangle for yourself, which is what my Student did - it is actually not that uncommon to create such a triangle without intending to.
For reasons given in Appendix 3 it is very unlikely indeed that you will ever encounter a situation where the use of the Sine Rule gives sin-1θ exactly 1 so that θ is exactly 90°.
If we look at the graph of cos θ against θ we see that the curve is very flat for values of θ less that 10° or more than 170° so a similar problem will arise. However it is very unlikely that you would create such a triangle without intending to.
This problem has interested me greatly, but after much searching I have not found anyone else who has described how it is possible to get a value of sin θ (or cos θ) greater than one without having made a mistake, and I think this is a pity.