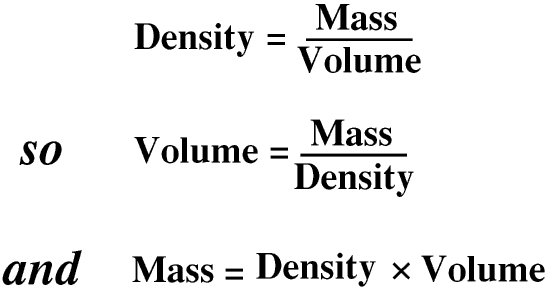
A term that was once in common use is specific gravity. This is the density of a substance compared with the density of pure water at 4oC. As this is 1 kg/dm3, if a substance has a density of 5 kg/dm3 it has a specific gravity of 5. Specific gravity is now seldom used for solids.
| Aluminium | 2.7 |
| Brass | 8.4 |
| Cork | 0.25 |
| Glass | 2.5 |
| Gold | 19.2 |
| Granite | 2.7 |
| Iron | 7.0 |
| Mahogany | 0.8 |
| Platinum | 21.4 |
| Silver | 10.5 |
When water turns to ice it expands: 10 cm3 of water make about 11 cm3 of ice. There is no change in mass, only in volume. The mass of 11 cm3 of ice is the same as the mass of 10cm3 of water, so the mass of 10 cm3 of ice is less than the mass of 10 cm3 of water. This means that the density of ice is less than that of water - which is of course why ice floats on water.
Most substances, solids, liquids and gases, expand when they are heated and of course contract when they are cooled. This means that there is a change in volume but not a change in mass, so when a substance is heated its density usually decreases.
For most solids, although the effect of this expansion on heating is very important indeed in many ways (not discussed here), the change in density is of no importance for most purposes. However, the change in density of liquids and gases when they are heated is very important indeed.
Although the litre is very widely used, and is the legal unit for the sale of petrol and many other liquids throughout Britain and Europe, it is not an official SI unit, and is therefore best avoided in scientific writing.
Most liquids expand a lot more than most solids for the same increase in temperature (which is of course why a mercury in glass thermometer works), and this means that a change in temperature will produce a significant change in density. So when we give the density of a liquid, for the most accurate work we also have to give the temperature at which the density was measured as well.
Most liquids are very poor conductors of heat (except mercury, which is a metal), and if we heat a liquid at the top the heat spreads by conduction through the liquid only very slowly. If however we heat it at the bottom the liquid at the bottom will expand as it is heated and become less dense than the liquid above it. It will therefore start to rise and the cooler liquid will sink to take its place - this effect is called convection. Convection cannot occur in solids but it is of enormous importance in liquids and gases.Water and, whatever some books may say, many other liquids expand when they freeze: this means that ice is less dense than water and so floats on water. Ice is a very poor conductor of heat and a layer of ice on the top of a pond will help to keep the water underneath from freezing.
Water does have one very unusual property: when cooled to below 4oC it expands rather than contracts, so it reaches its maximum density at 4oC. This is very important to pond life because in very cold weather it means that the water at the bottom of the pond will not fall below 4oC (unless the pond freezes solid). This property is called the anomalous expansion of water.
This table gives the density of pure water at different temperatures.| Temperature | Density |
| oC | kg/dm3 |
| 0 | 0.999 |
| 4 | 1.000 |
| 10 | 0.999 |
| 20 | 0.998 |
| 30 | 0.992 |
A Galilean Thermometer consists of a number of air-filled glass vessels. All the vessels have the same volume but each contains a very slightly different amount of a substance such as fine lead shot. As the temperature of the water increases its density and so buoyancy gets less and the heavier vessels will sink. The temperature of the water, which is of course also the temperature of the room, is given by that on the lowest numbered vessel still floating.
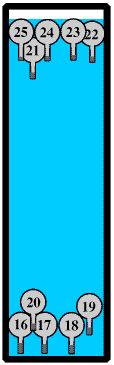
Although Galilean Thermometers are usually in a sealed container there must be a small air space at the top to allow the water to expand without cracking the container.
The vessels must be at either the top or the bottom, they cannot be in the middle. This is more fully discussed in the page on submarines - to link to it please click hereGalilean Thermometers are often confused with Lava Lamps but they do not work the same way. Lava Lamps work by convection but in a Galilean Thermometer there is no convection because all the water is at the same temperature.
If the water is not pure but has substances dissolved in it it will have a different density: most solids dissolved in water increase the density of the solution. The density of sea water is about 1.03 kg/litre.
We can measure the density of aqueous solutions by using a hydrometer. This is is similar to an angler's float: as the buoyancy of a liquid depends upon its density the denser the liquid the higher the hydrometer will float in the water. The density of water and aqueous solutions is often given as a specific gravity, the density of the liquid compared to the density of pure water at 4oC. So if the density of a sugar solution is 1.02 g/cm3 its specific gravity is 1.02. Specific gravity used to be widely used but now its use is usually restricted to water and aqueous solutions. The stem of the hydrometer is calibrated to give the specific gravity of the liquid.
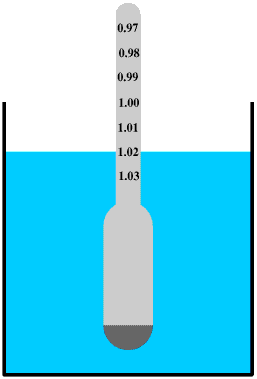
Wine-makers use hydrometers to check the sugar content of the grape juice before it is fermented - the higher the sugar content the greater the density of the grape juice.
Do not confuse a hydrometer with a hygrometer - a hygrometer is used to measure the humidity of the air.
Buoyancy is discussed in another Page of this Web Site - to read more about it please click hereGases expand a lot more than solids or liquids when they are heated. They are also compressible, that is, we can compress them into a smaller volume. For this reason whenever we give the density of a gas we must always give both the temperature and the pressure. We often give the densities of gases at the Standard Temperature and Pressure (STP) of 0oC and 1013 mb. At STP the density of air is about 1½ g/litre.
Some gases such as hydrogen, helium and methane, are lighter (less dense) than air, while others such as propane, butane and carbon dioxide are heavier than air. Hot air is of course lighter than cold air, so we get convection in air.
Gases which are lighter than air disperse very rapidly and so a leak of hydrogen or methane (ordinary gas) is not dangerous for more than a few minutes after it has been stopped and the windows opened. But gases which are heavier than air can collect in cellars and in drains and can remain there, and dangerous, for days or weeks. This is discussed in the page on storage of gases - to link to it click hereArchimedes, The King of Syracuse and the Golden Crown
Archimedes (287 - 212 BCE) is usually regarded as one of the three greatest mathematicians of all time, the other two being the German Carl Friedrich Gauss (1777 - 1855) and the English Isaac Newton (1642 - 1727). The next seventeen names on the list of the Twenty Greatest Mathematicians would almost all be Arabic, Indian or Persian.
Archimedes lived in Syracuse in Sicily, which in those days was a Greek Colony, with its own King. The King of Syracuse had ordered a new gold crown and had given his goldsmith the right amount of gold to make it. When the goldsmith brought the crown to the King it weighed the right amount, but some of his servants told the King that they had heard the goldsmith boasting that he had stolen some of the gold and replaced it with silver, so the crown was not pure gold but an alloy (mixture) of gold and silver.
The King sent for Archimedes and told him he was to find out whether this was true - but he must not damage the crown. Archimedes thought about the problem, which appeared quite imposssible to solve. While he was thinking about it he did not wash or change his clothes. After three days he smelt so strongly - Syracuse is a very hot place in the summer - that even he noticed, and he went to the Public Bath House. As he got into his bath he noticed the water rise up the sides, and suddenly he saw how to solve his problem. He jumped out of the bath and ran out of the Bath House shouting “Eureka! Eureka!” (the Greek for “I've found it, I've found it”) - in those days it was considered quite normal for old men with beards to run around the streets in broad daylight stark naked.Two thousand years after Archimedes we find it hard to understand what a major step forward his discovery was.
Today the simplest schoolboy is familiar with truths for which Archimedes would have sacrificed his life.
- Ernest Renan (1823 - 1892)
Archimedes realised that if a lump of gold and a lump of silver had the same heaviness the silver one would have a greater bigness, so that if the crown was made of a mixture of gold and silver its bigness would be greater than if it were made of pure gold but less than if it were made of pure silver. He took the crown and also lumps of pure gold and pure silver of the same heaviness. To measure the bigness of each he lowered them into a bath of water filled to the brim and collected the water that overflowed. He did not know how to measure the bigness of the water that overflowed, but he did know that the greater the bigness of the water the greater its heaviness, so he measured its heaviness. By measuring the heaviness of the water that overflowed he could show that the crown was bigger than it should have been if it had been pure gold, and then went on to work out the exact amount of gold the goldsmith had replaced with silver.
The King was very pleased with Archimedes. The goldsmith? He had his throat cut... But in those days you did not get rich and powerful, let alone stay rich and powerful, by being Mr Nice Guy.
This is a well-known story and lots of people (even lots of books) think it is the origin of Archimedes Principle. But Archimedes Principle is actually about buoyancy, something completely different. you can read more about buoyancy by visiting the Floating and Sinking Page.
© Barry Gray September 2008