We are often faced with a problem of the sort Is it possible for the postman to deliver letters to every house in the village without going down the same road more than once? or Can we draw this shape without taking the pen off the paper?

Today these sorts of problem are in fact very important, particularly in graph theory, cartography, decision mathematics (used for planning delivery routes and many other business applications) another branch of mathematics called topology, and in knot theory, which covers everything from Celtic Art to the layout of the very complex twisted threads which make up DNA. But of course in today's applications with hundreds, thousands or even millions of “roads” a computer is used.
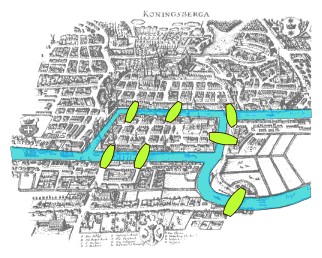
The first person to look at this problem from a mathematical point of view was the Swiss-German mathematician Leonard Euler (1707 - 1783) - Euler is pronounced oiler. He was invited by the citizens of Königsberg, a town in Prussia (a German State), to help them with their Bridge problem, which is why the problem is still called the “Bridges of Königsberg”. Königsberg was a town on the banks of and on an island in the River Pregel, and had seven bridges.
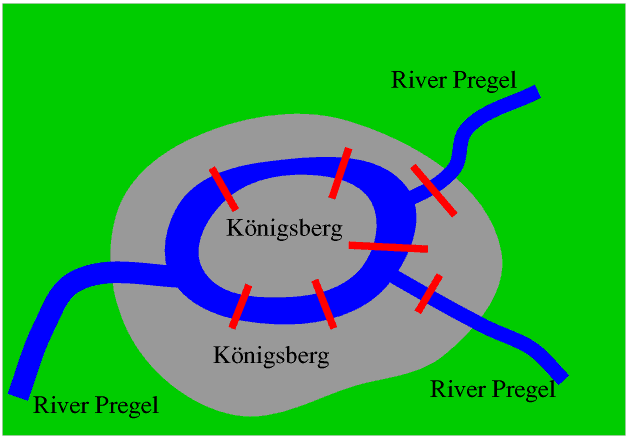
This is not a real map of Königsburg, just a drawing to help you understand the problem; there is an 18th century map of Königsberg at the end of this Page.
They asked him “Is it actually possible to start at a point and walk over all seven bridges just once and end up where you started from?” - lots of people had tried but no one had ever succeeded. He was able to show that it was impossible.
The key to understanding this sort of problem is to think about what happens at a junction (what mathematicians call a node).
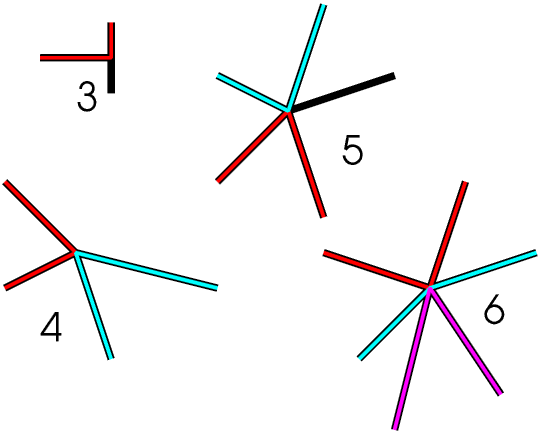
Every time you walk into and out of a junction you use up two roads, that is, you reduce the number of roads left for you to walk along by two. If there are an even number of roads meeting at a junction (an even node) you will eventually have used up all the roads, that is, you will have walked along every road leading into and out of the junction just once, but if there are an odd number of roads meeting at a junction (an odd node) you will eventually have just one road left so if you walk into the junction along it you will not be able to get out again. So you only need to look on the drawing for any odd nodes. It is best to draw a coloured circle round any you find. If there are no odd nodes you can always walk along every road just once, starting at any point (even “My House”) and returning to the same point (provided you take care not to return to it too soon).
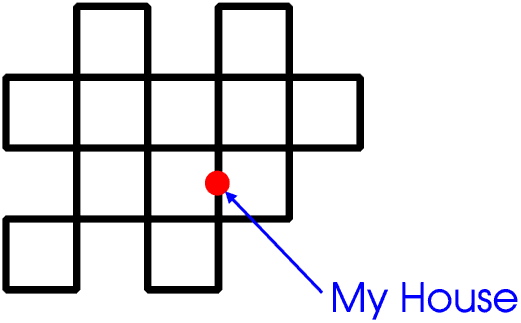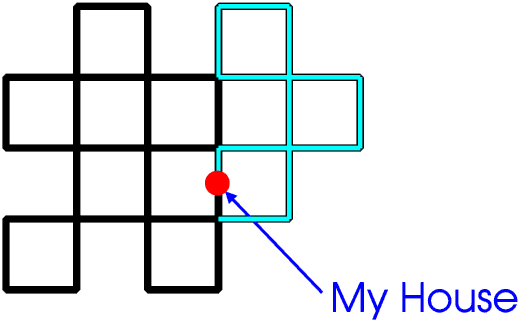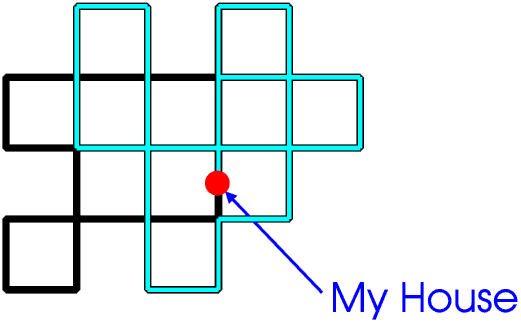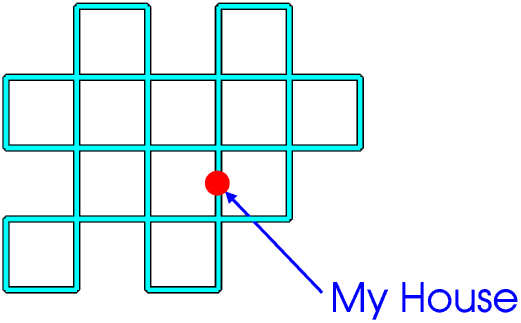
If there are two odd nodes you can walk along every road, but only if you start at one of the odd nodes and end at the other. But if there is any number of odd nodes other than two you cannot walk along every road no matter where you start. Try these three very simple layouts for yourself, then design some more complicated ones for you to try on your friends.

Sometimes in an exam a question on The Postman Problem may not be very carefully worded, so always make certain you have read it properly before you answer it. In particular check whether it actually says that you must start and finish at the same point.
So how did Euler prove that there was no answer to The Bridge Problem?He divided the town into four areas, the left bank, the right bank, the bit between the two river branches, and the island.
If you are standing on the Island you have five different bridges you can use to get off, that is, in effect, you are standing at the junction of five roads, and similarly for the other parts of the town.
He found there was not one, not two, not three, but four odd nodes, so the Bridge Problem was impossible.
Today a network is eulerian if it has only even nodes, and semi-eulerian if it has exactly two odd nodes.