Cartesian and Polar Coordinates

Polar and Cartesian (Rectangular) Co-ordinates

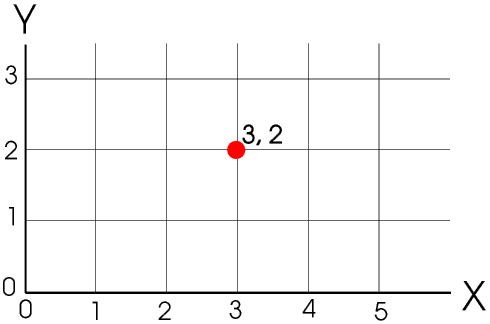
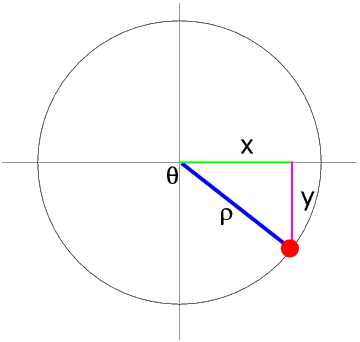
We can give the position of a point in two dimensions in two different ways.

Cartesian co-ordinates are named after the French mathematician René Descartes (1596 - 1650). The position of a point is given by its distance from the two axes (almost invariably called X and Y). Cartesian co-ordinates are also called rectangular co-ordinates, including on your calculator.

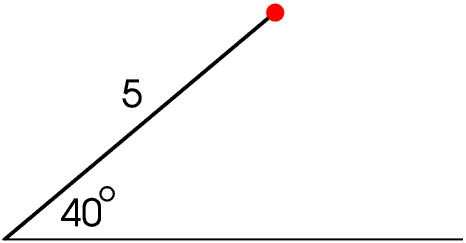
In polar co-ordinates the position of a point is given by ρ (Greek letter rho), its distance from the origin, and θ (Greek letter theta), the angle between the line from the point to the origin and the horizontal line through the origin. The length of the line is always positive and the angles are measured anti-clockwise. Polar co-ordinates

Compass bearings are usually measured clockwise from North but are not considered further here.

When we are plotting graphs in maths and science we usually use Cartesian co-ordinates, but in everyday life we actually use mainly distance and direction, that is, polar co-ordinates, even if we do not use those words.

We can measure angles in degrees or radians. On this Page all the examples are given in degrees. Radians are explained in the Page on Circles. Your calculator can work in radians or degrees and can convert between them.

Your calculator can also convert between polar and Cartesian co-ordinates - to read about how to do this click here.

A circle can be divided into four quadrants. In the First Quadrant θ is in the range 0° to 90°, and x and y are both positive.

The relationship between the Cartesian and polar co-ordinates of a point is given by
x = ρ cos θ
y = ρ sin θ

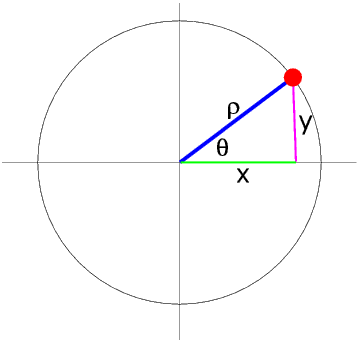
It is important to understand that this is the Rule for all values of θ, not only for values of θ between 0° and 90°.

We can see that sin θ = cos (90° - θ)

Try this for yourself on your calculator, for example check that sin 38° - cos 52° = 0. Throughout this Page I often give examples to try on your calculator: do please use them and even make up some more of your own. This will help you to understand what is happening and become familiar with doing the calculations.

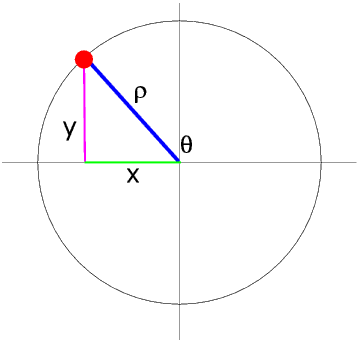
In the Second Quadrant θ is in the range 90° to 180°.

In the Second Quadrant y is still positive but x is negative so sin θ is positive but cos θ is negative. Try this for yourself, for example sin 111° and cos 156°.

We can see that sin θ = sin (180° - θ) and cos θ = - cos(180° - θ) - try this for yourself, for example where θ = 127°.

In the Third Quadrant θ is in the range 180° to 270°.

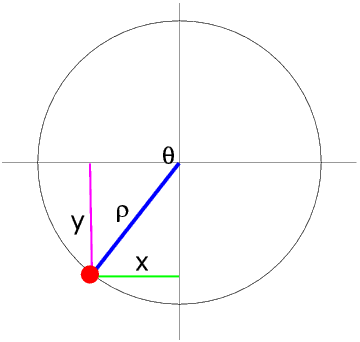
In the Third Quadrant both x and y, and so both sin θ and cos θ are negative.

We can see that sin θ = -sin (θ - 180°) and cos θ = -cos (θ - 180°)

In the Fourth Quadrant θ is in the range 270° to 360°.

In the Fourth Quadrant y is negative but x is positive so sin θ is negative but cos θ is positive - try putting some numbers in to prove this. We can see that sin θ = -sin (360° - θ) and cos θ = cos (360° - θ), again, try it for yourself.

Here are curves of sin θ and cos θ for θ from -100° to 500°.

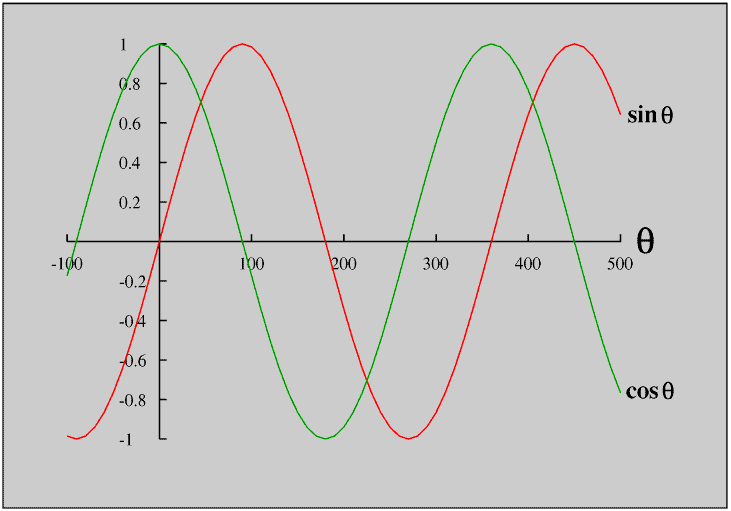
We can see that although the sine and cosine curves have the same shape, called a sine wave, they are 90° apart (are 90° out of phase).

If θ is greater than 360° we can see that sin θ = sin (θ - 360°) and cos θ = cos (θ - 360°) so the pattern repeats itself every 360°

Although for each value of θ there is only one value of sin θ and one of cos θ, for each value of sin θ and cos θ there are two values of θ (more of course if you include angles less than 0° or greater than 360°), in different Quadrants, and this is particularly important when we are using the Sine Rule to calculate the sides or angles of a triangle, as your calculator will only give you one of the values.

If a point is moving in a circle, so that ρ is constant, the graph of y against θ is a sine wave. If a point is moving in a circle at a constant speed (constant angular velocity), the graph of y against time will also be a sine wave. There are very many examples of sine waves in Nature, for example sound waves.

For reasons not explained here angular velocities are usually given in radians per second rather than degrees per second.