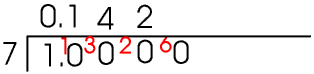
If we are dividing 1 by 7 we may lay the calculation out like this.
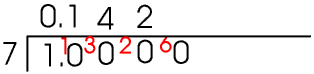
7 into 1 gives 0 remainder 1, so carry 1 into the next column. 7 into 10 goes 1 remainder 3, so carry 3 into the next column. 7 into 30 goes 4 remainder 2 so carry 2 into the next column. 7 into 20 goes 2 remainder 6 so carry 6 into the next column, and so on.
If at any stage it goes in exactly there is no remainder and the decimal terminates at this stage. If however there is a remainder the decimal continues. If we are dividing by 7 the remainder must be one of 1, 2, 3, 4, 5 or 6 - if it is 7 or more we have made a mistake.... This means that after at most six stages we must get a remainder that we have had before, so the pattern will repeat itself and we have a recurring decimal - the sequence when dividing by 7 is the six numbers 142857 142857 142857 etc. Similarly if we are dividing by 17 the remainder must be a number in the range 1 to 16 inclusive so the pattern will repeat after sixteen digits. Any common fraction can therefore be converted into a terminating or recurring decimal.
In practice 7 and 17 are very much the exception (which is why I chose them); for most numbers the decimal terminates or the sequence recurs before the maximum number of digits is reached, for example if we are dividing by 3 or 6 or 9 the sequence is only one digit long, by 11 it is two digits, by 27 it is three digits, by 101 it is 4 digits, by 41 it is 5 digits, by 7 or 13 it is 6 digits. If we are dividing by 17 the sequence does repeat every 16 digits, although your calculator cannot display them all at the same time so you need to use the scroll keys.The prime factors of 10 are 2 and 5. When we are doing a division every time we get a carry we introduce another zero, that is, we are making a number divisible by 10, so we can see that if we are dividing by a number whose only prime factors are 2 and 5 (for example 16, or 25,or 40) the division will always eventually terminate.
But if we are dividing by a number with any prime factor other than 2 or 5 (for example 3, 6, 7, 9, 11, 12, 13, 14, 15, 17 etc) it will recur.
When we are writing or printing recurring decimals we show the sequence of numbers by putting dots over the first and last numbers in it. On modern scientific calculators you can display recurring decimals in this way in maths mode,just use the recurring decimal button.
Take particular care with recurring decimals when you are using your calculator in maths mode. For example if you do not notice the dot when you do 205 ÷ 9 you might think the answer is 22.7, but of course to one decimal place it is 22.8.

Every recurring decimal can be converted into a proper fraction in the same way, so every recurring decimal is a rational number. But if the original decimal was, say, the recurring decimal value of 13 ÷ 17 the recurring sequence would have sixteen digits so there would be 16 nines on the bottom of the fraction before you start to simplify it. But if your calculator allows you to enter recurring decimals it does all the work for you, just use the recurring decimal key followed by the SD key. But remember converting a recurring decimal into a common fraction may be in the non-calculator paper.
It is useful to remember that the only prime factor of 9 is 3, the prime factors of 99 are 3 and 11 and the prime factors of 999 are 3 and 37.
There is one matter relating to recurring decimals which some people have difficulty with. 1 ÷ 9 = 0.111111111 etc so 9 × (1 ÷ 9) = 0.9999999 etc. But 9 ÷ 9 = 1 so 0.9 recurring = 1, not approximately but exactly.
Leading on from this, if we have a rope and measure its length as 3 m to the nearest metre, most people can see that the minimum length of the rope is 2.5 m, because if it were less than 2.5 m we would round it down to 2 m. The rope could be 3.49 m because if we measured it as 3.5 m we would round it up to 4 m. But it could be 3.499 m or 3.4999 m or in fact 3.49 recurring m. So the length of the rope is in the range 2.5 m to 3.5 m inclusive.
