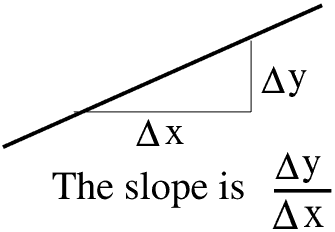
In mathematics the slope of a straight line is the ratio of the change in y to the change in x

For a curved line the slope at any point on the line is the slope of the tangent to the line at that point.
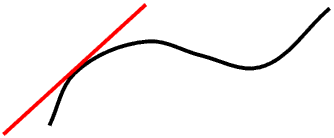
In each case the slope is the tangent of the angle the straight line makes with the horizontal.
But for thousands of years people we now call civil engineers, people who build aquaducts and canals and roads and railways etc, have always used gradients rather than slopes.
Today when we think of aquaducts we usually think of the huge stone arched structures the Romans built to carry water across valleys, many of which are still standing today, in many parts of Europe and North Africa. These carried not drinking water but bath water, that is, water for the great Roman Bathhouses. The aquaduct was in fact the whole channel in which the water ran, from the spring in the mountain to the town, it is just that two thousand years later only the massive stone arches used to carry the aquaduct across a valley have survived.
These arches were needed because an aquaduct must be downhill every centimetre of the way: if it is not downhill for even a centimetre the water just overflows over the sides. This means that every part of the route must be very carefully planned.
Two thousand years before the Romans the people of Mesopotamia (the then very fertile land between the River Tigris and the River Euphrates, approximately modern Iraq) were building aquaducts (canals) to carry water from the mountains and hills to irrigate their fields.
