You can use the memory of your calculator in four main ways. You will never get the most out of your calculator unless you learn to use them.
Every time you press the = key the result is stored. You can display it or use it by pressing the ANS key. The answer is stored until you do another sum, even 0 =, or you can clear it by using CLR and then selecting option 2 or 3. It is preserved if you press DEL or AC or turn your calculator off.
The answer is always stored to full (internal) accuracy, that is, exactly if possible otherwise to about fifteen significant figures.
It is most valuable (in fact indispensible) when you need to use the result of one calculation in another. Unless the answer is a one or two digit integer never do one sum and write the answer down and then type it into another sum: it takes time, you are quite likely to make a mistake and you will lose accuracy.
We have triangle ABC. Angle B is 48°, c is 39 mm and b is 30 mm. Find the other side and the two other angles. Give your answer to the nearest millimetre or degree.

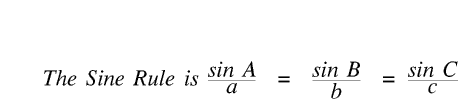
The Sine Rule is explained more fully on the Sine and Cosine Rule Page.
sin C = c × sin B ÷ b Your calculator says 0.9660882731 and this is stored in Ans. You need not write it down but to two decimal places it is 0.97.
So C = sin-1 Ans Your calculator says 75.03600371 and this is stored in Ans but you will write down 75°
A = 180 - 48 - Ans Your calculator says 56.963399629 and this is stored in Ans but you will write down 57°
Now a = sin Ans × b ÷ sin B Your calculator says 33.84222514 but you will write down 34 mm.
If you had entered rounded values into your calculator rather than using the Ans key (you were not seriously thinking of entering each of the three numbers to ten digit accuracy?) you would have found that C is 76° and then A is 56° and a is 33 mm
If you need to use an answer more than once you can store it in one of the Variable Memories, described later.
You can use Ans in many ways, for example in iterative calculations. Suppose a radioactive source has an initial activity of 26433 Bq and a half life of 21 minutes you could plot the activity against time by entering 26433 = and then Ans ÷ 2 = Then every time you press = it halves the previous answer. But there are lots of other ways where the Ans key is useful.
You can get back to and edit or use a previous calculation by using the upward arrow on the cursor control key.
There is a limit to how many calculations you can store in this way. Most characters take up one byte of storage but some take two or even three, and there is a limit of 200 bytes.
The calculation history is cleared when you press the ON or OFF or AC or CLR keys or change any of the modes or settings.
There are eight of these,labelled A, B, C, D, E and F and X and Y. They all work in the same way. Some people like using X and Y in algebraic calculations but you do not have to, and I find A to F in a slightly more convenient place on the keyboard. (M is the Independent Memory. It works in a similar way but has a slightly different use, described later.)
To store a number in a variable memory you use the Store (STO) key - use the shift key first of course. To store 23 in memory B you would enter 23, then press STO and then the key with B over it: the B is in red but you do not have to press the red ALPHA key. If the number is already in your calculator, for example the result of a calculation you just need to press STO B. The display shows 23→B or of course Ans→B
To display the value of B you press RCL and then B without pressing the ALPHA key, to use the value of B in a calculation you just press B, but this time you must use the ALPHA key.
Remember before you use a variable memory key you must press one but only one of STO or RCL or ALPHA
We can use Trial and Improvement to find the value of x to two decimal places when x3 - x = 9
This is a time when we might find it helpful to use Fixed Point, to three decimal places. To do this press Setup (use Shift of course) then select 6 for Fix then 3 for 3 decimal places.
We might start by trying x = 1 so enter 1 into B

Now enter B3 - B This will stay in your calculator’s memory unless you press ON, OFF or AC or CLR or use the Mode or Setup keys.
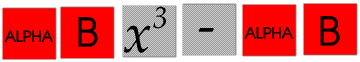
Now each you press = it will do the sum using the value stored in B, in this case 1 so you will get the answer 0.000
Store 2 in B, as before, and then use the upward arrow to bring the sum back. Pressing = will give the answer 6.000.
Try 3, this will give 24.000. Try 2.2, this gives 8.448, which is a little too low, try 2.3, this gives 9.867, which is too high. Try 2.24, this gives 8.999 which is very slightly too low. We need to find whether the answer, to two decimal places, will round to 2.24 or 2.25, so try 2.245, the half-way point, this gives 9.070 which is too big so the answer is 2.24
When you have finished do not forget to cancel Fixed Point. Press Setup, then select 8 for Norm, then 1 (the use of 2 is discussed on an earlier Page, under Standard Form.)Until the coming of the pocket scientific calculator Trial and Improvement, sometimes called Trial and Error, was so tedious and time-consuming that it was very seldom used if any other method was available, now it is so quick and easy that it is a routine way of doing many calculations even where other methods are available.
Plot the curve 2x2 - 5x + 7 for values of x from 0 to 3 at 0.2 intervals.
If you have TABLE mode on your calculator you can use that, but here is how to do it if you do not.First set your calculator to fixed point with one decimal place, then store 0 in B
We do the calculation in three stages. First we use the stored value of B in the sum, then we increase the value of B by 0.2, then we store the answer in B, then we repeat the whole thing using the new value of B.We do this by using the multi-statement facility, where we enter several sums on a single line separated by colons (Use the ALPHA key of course).
Try 3 + 4 : 4 + 5 : 5 + 6
When you press the = key it does the first sum, press it again and it does the second sum, again and it does the third sum, again and it does the first sum again.
You do need to bear one thing in mind. If you enter 3 + 4 your calculator (or computer) will just sit there: it does not know whether you mean 3 + 4 or 3 + 43 or 3 + 4 + 5 The only way it knows you have finished entering the sum is when you press : or of course = But STO B and RCL B are complete in themselves, your calculator will know you have finished and so will start working the moment you enter the B

Remember that you do not press the ALPHA key before the final B. The moment you enter the B your calculator will do the sum 2B2 - 5B + 7 using the value you stored in B, that is 0. It will display 7.0. When you press = it will do the next calculation, that is, add 0.5 to 0 and display the answer 0.5 When you press = again it will store the answer 0.5 in B but will still display 0.5. When you press = it will start over again, but this time using the new value of B.