For any triangle we can use the Sine and Cosine Rules to calculate all the sides and all the angles if we are given
If we are given one side and two angles we do in fact know all three angles because all the angles add up to 180°, and so calculating the third angle is always the first thing we do.
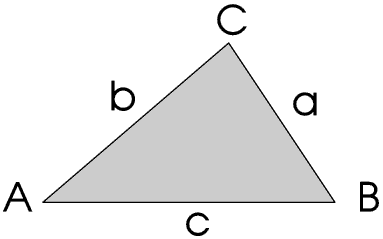
We usually label the angles of a triangle with capital letters, usually consecutive letters such as ABC or PQR, and the length of the sides with small letters. Side a is opposite angle A.

A triangle may be acute, obtuse or right angled. In an acute angled triangle all the angles are acute. As all the angles in a triangle add up to 180°, if one angle in a triangle is obtuse (an obtuse angled triangle) or a right angle (a right angled triangle) then the other two angles must be acute. The longest side is opposite the biggest angle.
The Sine Rule is very easy to remember and to use.
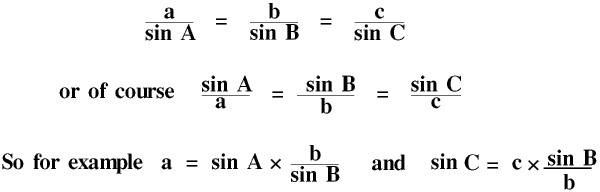
We can always use the Sine Rule if we know one side and its opposite angle, and either one more side or one more angle.
Of course you might have triangle MSG not ABC, but then the Sine Rule is sin M over m equals sin S over s equals sin G over g, which is just as easy to remember.
We use the Cosine Rule if we cannot use the Sine Rule. It has two forms. In most exams both forms will usually be on the Formula Sheet given to you with the question paper so you do not need to learn it by heart.
If we are given three sides and need to find the angles we use this form.
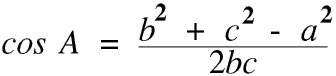
Then we can use the Sine Rule to find the other two angles.
If however we are given two sides and the included angle (the angle between them) we need to find the third side before we can find the other angles, so we use this form.
Then we can use the Sine Rule to find the other two angles.
Some people get a little confused using the Cosine Rule if they have triangle KMQ rather than ABC. Just remember that K and k, M and m, and Q and q are opposite each other. We use the Cosine Rule if we are given two sides and either the angle between them or the third side. So if we want to find M or m these are A or a, the other two sides are always b and c. So m2 = k2 + q2 - 2kq cos M. If you are not certain about what to do never be afraid to draw the the triangle on a piece of paper and write in A B and C.
Everything that follows on this Page assumes you have a scientific calculator, and that you understand and can use the Ans key. As most square roots and sines and cosines are irrational numbers (irrational numbers are explained on another Page) almost all calculations involving the Sine and Cosine Rules will involve irrational numbers at some stage and your calculator will give the result to 10 figures. If you write them all down you will lose marks in an exam, waste a lot of time, and probably make a mistake, so you need to round the result sensibly before you write it down. On this Page all data and results are given in millimetres to the nearest millimetre or degrees to the nearest degree. But when you are using the result of one calculation in another calculation you must always use the full ten figure result: remember it is always stored in Ans.
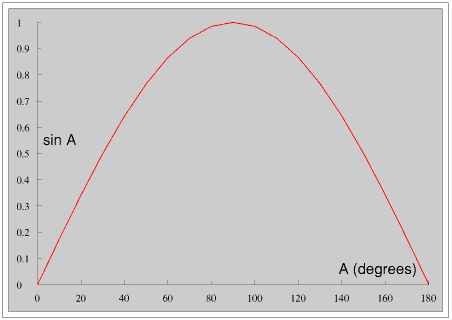
All the angles in a triangle must be between 0° and 180°. Here are graphs of sin A and cos A for values of A between 0° and 180°.
If we are given a, b and c we use the Cosine Rule to find the first angle. The largest angle faces the longest side and can be acute, a right angle or obtuse, but whatever it is once we have found the largest angle we know that the other two angles are acute. We can use the Sine Rule to find them, the order we find them in does not matter.
If we are given a, b and C we need to find c using the Cosine Rule. We now have all three sides so we use the Sine Rule to find the other two angles. We know that the smaller of the two remaining angles must be acute, so we find that first.
If we are given a, b and A, if a is bigger than b then we know A is bigger than B so B must be acute. C can be acute, a right angle or obtuse but we know it without using the Sine Rule once we have found B.
If we are given a, b and A and b is equal to a then the triangle is isosceles so we can find the other two angles without using the Sine Rule.But if b is bigger than a then B is bigger than A, and, unless we have any other information, we cannot know whether it is acute or obtuse so we must consider both possibilities. This is discussed at some length in Example 10.
In any triangle sin A must be in the range 0 to 1 and cos A must be in the range -1 to +1. If we find a value outside these ranges when we are using the Sine or Cosine Rules the most likely explanation is that someone has made a mistake somewhere. So first we should first check our measurements and calculations. Then we should check that the triangle can actually exist: three “impossible” triangles are described at the end of this Page. But there is also another possibility, described in Example 11. Sadly, most people do not consider this possibility.
Several worked examples follow, and each deals with a different situation. You might find it helpful to print the ones you might need to help you with a specific problem, so that you can make some notes on it.
In the first four examples all the angles are necessarily acute. I have drawn each triangle fairly accurately.
In the next three examples we are given an obtuse angle. Again I have drawn each triangle fairly accurately.
In the next three examples one of the angles to be found is obtuse, but in order to make sure you really understand what you are doing I have deliberately not drawn the triangle accurately.
If we are given two angles and one side we can find the third angle without using trigonometry at all, so it makes no difference whether the angle to be found is acute or obtuse, see Example 6.
The last example, for Advanced Readers only, relates to a problem I have never seen explained, in any text book at any level or on any web page. If you encounter it in a question in a maths exam at or before normal school leaving age it will only be because the person who set the question is totally incompetent.
We can “solve” a triangle, that is, find all the sides and all the angles, if we are given three pieces of information, three sides and no angles, or two sides and one angle, or one side and two angles. But except in the special case of an equilateral triangle, when we do not need to use trigonometry at all, at least one of the calculations will produce an irrational number. So if we measure or are given four pieces of information we need to be aware that they cannot all be 100% accurate. For example, if we have three sides and one angle we can calculate the second and third angles using either the Sine Rule or the Cosine Rule, but the two methods will not give the same result.
Case 1
If we are given three sides any two two of them must add up to more than the third.


Case 2
But suppose we are given two sides and one angle not the included angle.
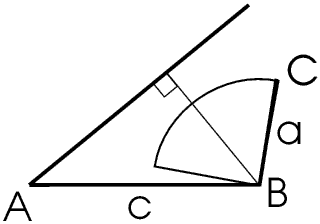
Here we are given A, a and c. C lies on the arc drawn. The length of the perpendicular line added to the drawing is c × sin A. IfAngle A is acute we can see that if a is shorter than c × sin A no triangle is possible.
In fact, because the sine of any angle cannot be greater than 1 a must be greater than or equal to c × sin A in any triangle whether A is acute or obtuse.The case where a is very close to c × sin A is discussed at some length in Example 11.
Case 3
All the angles in a triangle add up to 180°, so if we are given one side and two angles the two angles we are given must add up to less than 180°.