More about irrational numbers

π and most square and other roots, trigonometrical functions such as sines and cosines, and logarithms are all irrational numbers.

There are many different ways of expressing π and they do not look the same at all, but here is the simplest and the one which makes irrational numbers easiest to understand.

so it never either recurs or terminates and cannot be expressed in the form a ÷ b.

All irrational numbers take the form of a convergent infinite series like this. How mathematicians eventually arrived at these series is quite fascinating and is explained in most books on the history of mathematics and on several web sites - try a search on “Value of pi” or, more interestingly, “ The square root of 2” - but the maths is very advanced and if you can follow it you will probably not be reading this Page (except perhaps as a critic - please e-mail me with your comments).

Here is the simplest series for the square root of 2 - as for π there are others and they all look quite different.

Here is the scattergram obtained by calculating the value of this series for different numbers of terms (starting with the second term).

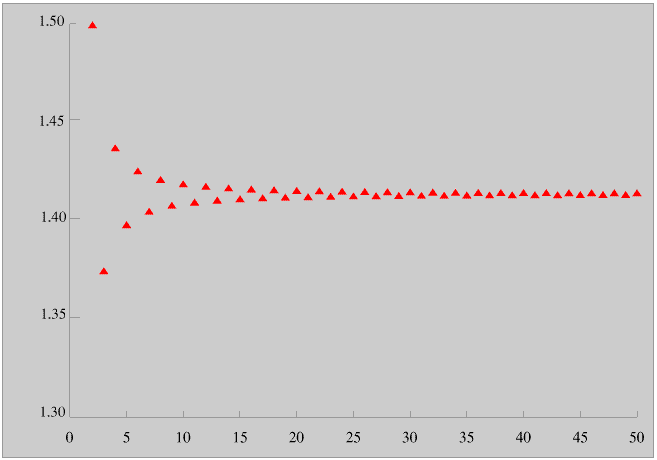
This scattergram explains more clearly than words can the meaning of convergent infinite series. As we increase the number of terms used the values get closer and closer together. But if you use a hundred terms there is always some bright spark who will say “Sucks to you, I’ve used a thousand”. Someone calculates the square root of two to a million places of decimals, then someone else comes up with five million. Here it is to five million places of decimals if you are interested...

The true nature of irrational numbers as convergent infinite series was not understood until the 19th century, but attempts to find approximations for the values of π, square roots and trigonometrical functions had been made for thousands of years before then. Four thousand five hundred years ago a Pharaoh called Sneferu, who was King of Egypt from 2575 to 2551 (BCE of course!) was the first Pharaoh to build a true pyramid, with a square base and smooth equilateral triangle sides. We can use trigonometry to show that the slope of the sides should be 54 degrees 44 minutes: the slope of the sides of his pyramid was 54 degrees 27 minutes, less than half of a degree out! Try just drawing an angle this accurately, then imagine building a pyramid with a base of 185 m this accurately out of stone blocks, using only the tools and materials that were available 4500 years ago!

The values of sines and other irrational numbers have been needed by architects, navigators and astronomers and many other people for thousands of years, but few of these people have ever been sufficiently good mathematicians, or more importantly could afford the time, to produce their own values. Instead a small number of mathematicians did the calculations and published their results as Mathematical Tables. The earliest published Tables go back two thousand years, and Tables were still the standard way of doing calculations involving irrational numbers until the introduction of the scientific calculator in the 1970s. Usually 4 figure tables, that is, giving values to four significant figures, were used. Looking up values in these Tables was tedious and time-consuming, and at school only the most able students were trained in their use. Today however anyone can do in a few seconds a calculation which forty years ago would have taken several minutes and been beyond 80% of the population - and to 10 rather than 4 figure accuracy.

The series for π given above is perhaps the simplest of all convergent infinite series to understand but it converges very slowly - try it for yourself. So it is not one of the series actually used for calculating π.