
When we count on our fingers we are using natural numbers, which is why in Early Years Teaching natural numbers are sometimes called counting numbers. We usually use N to stand for a natural number.
Natural numbers are fine if you just want to count sheep, but if you are Pharaoh of Egypt living four thousand five hundred years ago and want to build a square based pyramid with a base of 185 m and smooth equilateral triangle sides first you need to calulate the slope of the sides, and to do this you need a totally different set of mathematical tools. (The answer is 54 degrees 44 minutes if you are interested.) And this is the reason why many people find some aspects of mathematics difficult.
“God made natural numbers, all the rest are made by Man.”
Leopold Kroneker (1823 - 1891)
All numbers other than natural numbers are just tools Man has designed to help him solve problems he could not solve without them. If you lose sight of this, or more sadly if you were never taught this, some branches of mathematics may appear confusing or illogical.
The way in which Man first learned to use numbers as tools is described on the Subitizing Page.
Because when we are counting we always start with one, zero is not a natural number, and the Egyptians, Greeks, Romans and most other Ancient People had no symbol for it.
Natural numbers were once called cardinal numbers and you may still come across this term.

Ordinal numbers are 1st, 2nd, 3rd, 4th etc, where we put things into order. There is no zeroth: the day before the 1st of June is the 31st day of May not the 0th of June.
(There is however a Zeroth Law of Thermodynamics, but only because someone discovered one of the Laws of Thermodynamics and called it the First Law, and then somebody else discovered another Law which should have come before it.)

Integers are whole numbers, and include negative numbers and zero. We usually use n to stand for an integer.
Examples of integers are

When Mrs Wilson takes Kingfisher Class to the Swimmming Pool, if twelve boys and eleven girls get into the water then she must make certain that twelve boys and eleven girls get out of the water, not more or less, not approximately, but exactly. She is using natural numbers. But once we stop counting and start measuring we have entered the world of real numbers.
“Fred, what’s the floor area of this room?”
Fred looks up. He estimates the room is about 3 m long and 4 m wide. He knows his times tables so he replies
“About 12 m², Charlie.”
“I want it more accurately than that, Fred.”
Fred has only estimated the size of the room to the nearest metre. He finds a 100 cm ruler and measures the room with it, to the nearest 10 cm (0.1 m). He finds it is 3.2 m by 3.9 m. He gets out his pocket calculator.
“About 12.48 m², Charlie.”
“I want it more accurately than that, Fred”
Fred goes upstairs and gets a tape measure. He remeasures the room to the nearest centimetre. It is 3.18 m by 3.93 m.
“About 12.4974 m², Charlie.”
“I want it more accurately than that, Fred.”
Up to now Fred has assumed the room is rectangular. He realises that if he wants to measure the area of the room to the nearest mm2 he needs to take into account that the corners may not be exactly right angles and the walls may not be exactly straight.
“Charlie, why exactly do you want it more accurate than that?”
“I’m thinking of buying a new carpet.”
“Doh”
In the real world we cannot always be 100% accurate and we do not always need to be, we just work to the level of accuracy appropriate for the task. Most of the time we do this without consciously thinking about it. For example
“How far is it to Platter’s Farm?”
“About one and a half kilometres.”
“Thanks.”
On the other hand, the SatNav system in your car contains electronics which must be able to measure the time taken for a radio signal from a satellite 12 000 km away to reach you to an accuracy of better than one thousand millionth of a second.
Real numbers have a position on a number line.
Why real numbers? See the Section on Complex Numbers - but please not until you have read the next Section.

We live in a World of Tick Boxes. We tick boxes when we fill in a form or take part in a survey, these days even when we take an exam! We like to put everything and everybody into neat pigeonholes; even our feet have to be a certain shoe size. But these Tick Boxes and Pigeon Holes and Shoe Sizes are entirely Man-made, for our own convenience. The Real World is not really like that: our left foot could be a size 5.07 and our right foot a size 4.93.
Two thousand years five hundred years ago the Ancient Greeeks also liked everything to be nice and neat and logical. They did not have pocket calculators, not even decimals, so maths was about common fractions: one half, two thirds, three fifths, four sevenths etc.
The problem was, some numbers, such as the ratio of the circumference of a circle to its diameter (now known as π) or the ratio of the diagonal of a square to its side (the square root of two), did not fit into this nice neat way of doing things. For example, one squared is one and two squared is four so the number whose square is two (that is, the square root of two) must be between one and two. We can try to find this number by trial and error - this is not easy if you can only use common fractions. Here is a start.

You are welcome to continue it. The Ancient Greeks did not have calculators so of course I have not used one

and neither should you. You can make things even more realistic by using Ancient Greek numbers: if you do not know these you can use Roman or Ancient Egyptian numbers instead. I prefer Ancient Egyptian numbers, I think they are prettier, and you can see them on my Ancient Egyptian Maths Page.
Of course you will not do any better than the Ancient Greeks: there is no fraction which when squared makes two. (Remember that decimals are only common fractions in which the denominator is always 10, or 100, or 1000 etc.) The Ancient Greeks did not like this at all. In fact it was another two thousand years before mathematicians finally came to terms with the idea that a number which cannot be expressed as a common fraction, in the form a ÷ b where a and b are integers, can still be a real number, with a real position on a number line.
Today a rational number is a number that can be expressed exactly as a ratio (that is, a ÷ b) and an irrational number is one that cannot be.
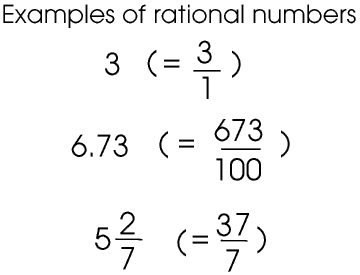
Irrational numbers are real numbers and have a real position on a number line, and we can express them to any degree of accuracy we like, whether one or two decimal places, or ten or twenty or a million. It is just that they do not conform to the Rules the Ancient Greeks made for a Nice Neat World, in the same way that your feet probably don’t conform to the Rules we have made for Nice Neat Shoe Sizes.
It is quite easy to show that an irrational number is a real number with a real position on a number line. Consider the square root of 2 for example. 1.4142² is 1.99996 and 1.4143² is 2.00024, to 5 decimal places.
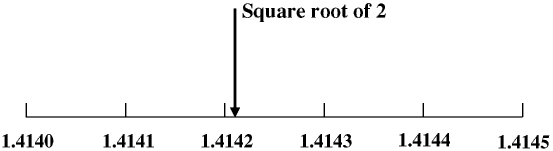
Although there are lots of irrational numbers other than square roots, if you are asked questions about rational and irrational numbers in a GCSE or other school-leaving exam any irrational numbers in the question will almost always be square roots. Then just remember that even though the square root of a rational number may be irrational, the square of the square root of a rational number is always rational. Sounds obvious when it is put like that!
Until the early 1970s, when scientific pocket calculators began to become readily available, calculations involving irrational numbers such as square and other roots, logarithms, and trigonometrical functions such as sines and cosines, were tedious and time consuming, usually involving the use of books of four figure mathematical tables, and very few people worked with them to an accuracy of better than four significant figures. Today’s scientific calculators have function keys for π and all the other irrational numbers, which give the values of them to ten significant figures. So now even schoolchildren can use a scientific calculator to obtain instant and highly accurate answers to problems involving irrational numbers without needing to know anything about them: for most people living in the 21st century the difference between rational and irrational numbers is of no practical importance at all. But if you do need, or want, to know more about irrational numbers then there is more about them, and the difference between irrational numbers and recurring decimals, in a later Section of this Page.

This Paragraph is really included only for completeness, to explain why we need to use the term real number. Do not worry if you cannot understand how complex numbers can be important, just re-read the opening paragraphs of this Page and then remember that complex numbers are just tools which some people find useful.
In Nature many things, from sub-atomic particles to galaxies, move in curved paths. Here is an equation for a typical second order curve.
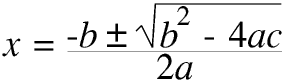
Never forget that Man made the Rules. We all know that 2 × 2 makes 4 but we have also decided that -2 × -2 should also make 4 (+4 of course). The plus or minus is needed in this equation because every (positive) number must have two (real) square roots, one positive and one negative. But going one stage further, according to our Rules there can be no real number, positive or negative, which multiplied by itself makes a negative number, that is, the square root of a negative number cannot be a real number. We call the square root of a negative number an imaginary number.
A complex number consists of two parts, a real part and an imaginary part. The solution to this formula is complex if b² - 4ac is negative.To some people complex numbers are very important indeed and a whole branch of mathematics is devoted to them. The value of the square root of -1 is so important that it is given its own symbol, i. To quantum physicists i is as important as π is to the rest of us.
However most of us are not quantum physicists, and most people do not come across complex numbers unless they are studying maths beyond normal school leaving age. You can buy calculators which handle them (I have one of course) but a Casio fx-86 will not and if you try to find the square root of a negative number on one you will get a syntax error.
