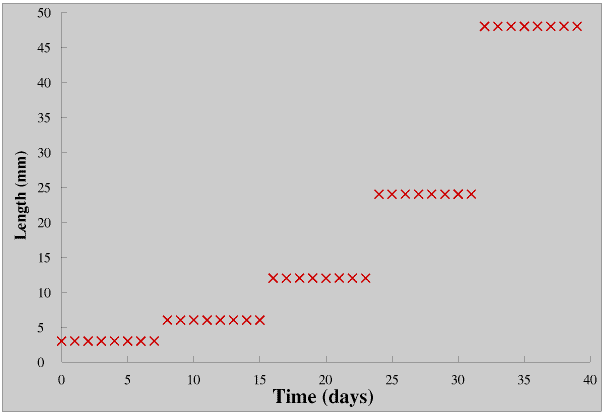
This Page follows on from other Pages on logarithms, but because you can also link to this Page from the Page on Radioactivity and Half Life it includes the graphs of James’s Plant and Albus’s Caterpillar from the earlier Pages for the benefit of those who have not already come across them. If you are unfamiliar with logarithms you might like to read An introduction to logarithms before you go any further.
Mathematicians talk about an exponential series, 1, 2, 4, 8, 16, ... 2(n-1), ... where n is an integer. (Remember that n0 = 1) It is called an exponential series because n forms part of the exponent.
Albus’s caterpillar is doubling its length every eight days so it is growing exponentially in this way (but only until it is fully grown of course).

In the Real World, outside mathematicians’ Ivory Towers, exponential series like this, where things change only in discrete steps, are not common. Much more common are growth patterns which are continuous, like James’s plant.
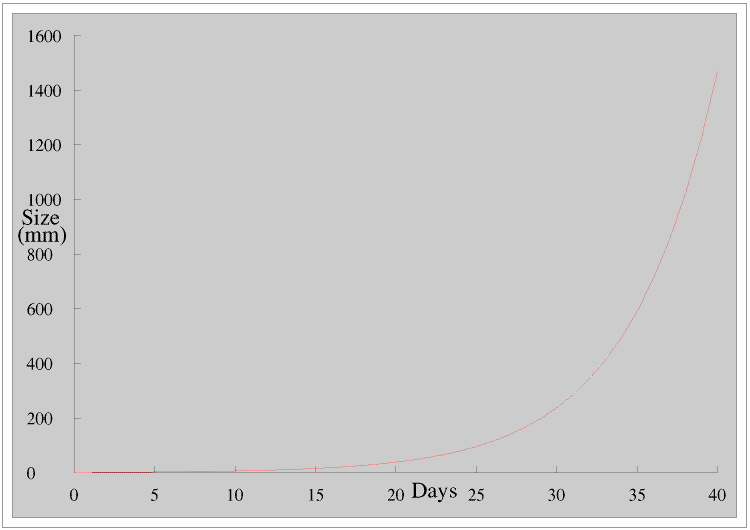
Exponential growth of this sort starts very slowly but then increases very rapidly: the shape of the curve is often referred to as like a letter J.
James’s plant is doubling its diameter every four days, for example it doubles its diameter between days 15 and 19 but it also doubles its diameter between days 31 and 35. You can see this more clearly if we use a logarithmic scale for the diameter.
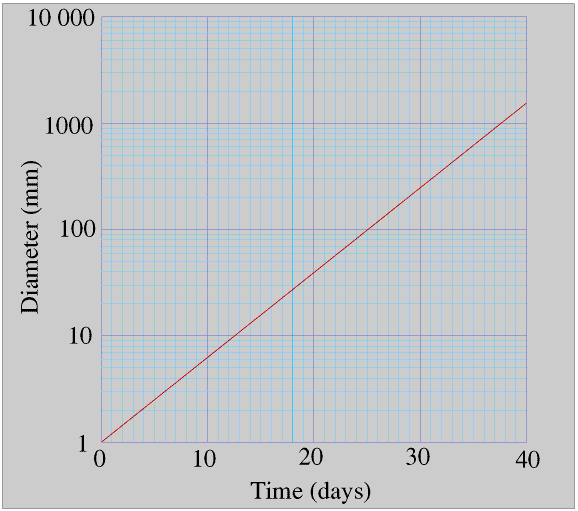
This graph makes it easy to see that (and also understand why) there is nothing special about the number two in exponential growth. For example James's plant doubles its diameter every four days but it also trebles its diameter about every six days - check this out for yourself. The only reason why we almost invariably use 2 rather than 3 or 5.71 in simple calculations involving exponential growth (and more particularly decay) is that most of us would rather multiply and divide by 2 than by 3 or 5.71!
It has been calculated that if a pair of blowfly emerged from their pupae on March 1st, and mated as often as they could and laid as many eggs as they could, and all the eggs hatched and eventually became blowfly, by September 30th the entire surface of the Earth would be covered by blowfly to a depth of 17 metres! Of course this does not happen, because lots of birds and other animals eat blowflies and blowfly larvae: if there are lots of blowfly the birds say “goody goody” and eat lots and lots and then go home and make lots of babies. When rabbits were first introduced to Australia they had no natural predators so for a time the population increased exponentially. But exponential growth stopped when they started running out of food. In Real Life a truly exponential population growth phase does not usually last for very long because of the effect of other factors.
Exponential decay is similar to exponential growth. Here is the graph of the radioactivity of a sample of a radionuclide which loses half of its radioactivity every five days.
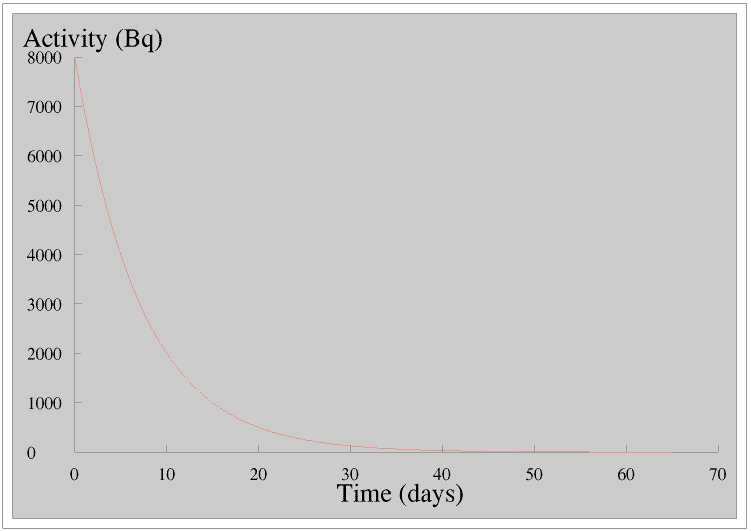
Compare this with the graph of the growth of James’s plant.
Many substances in Nature are radioactive. We often talk about the half-life of a radionuclide, for example the half-life of bismuth-210 is 5 days. This means that if we take a sample of bismuth-210 and measure its radioactivity, five days later its radioactivity will be half of this - whatever the size of the sample. Remember that half-life is for a particular radionuclide not an element, for example we cannot talk about the half-life of bismuth, only the half-life of a particular radioisotope of bismuth, for example bismuth-210. This is more fully discussed on the Page on Radioactivity.
Radioactivity is important in its own right, but it is also a unique example of perfect exponential decay unaffected by any other factors, which is why when we are learning about exponential growth and decay we usually study radioactivity.
When we are studying exponential decay sometimes we only need to use the concept of half-life. For example, we measure the radioactivity of a specimen at 6968 counts per minute and 57 minutes later it is 871 counts per minute. What will the radioactivity be in another 95 minutes?
First we divide 6968 by 871 to get the answer 8. This is 23 so 57 minutes is 3 half-lives, so one half-life is 57 ÷ 3 or 19 minutes. Then 95 ÷ 19 is 5 so 95 minutes is 5 half-lives and 25 is 32 so the radioactivity is 871 ÷ 32 or 27.2 counts per minute.
Calculations involving exponential growth can be done in exactly the same way, except of course that we multiply rather than divide.
This is fine if the times involved are whole numbers of half-lives. If this is not the case the maths gets more difficult. You might not need to learn about it for your school exams, but if you do, or are just interested, here it is. It is important in Real Life because if you are dealing with radionuclides with half-lives measured in thousands of years (for example carbon-14, used in carbon dating, has a half-life of 5370 years) the times you are working with will not usually be whole numbers of half-lives...
The rest of this Page is still under construction.