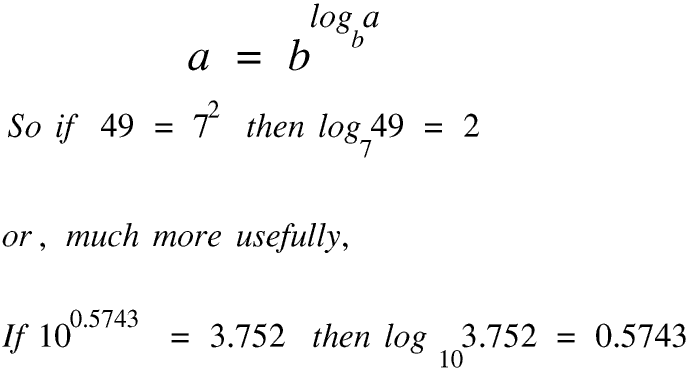
Logarithms have had, and still have, many uses, and the following Pages discuss some of them.
Logarithms were invented by the Scottish mathematician John Napier (1550 - 1617). The logarithm of a number to any base is the power we must raise the base to in order to get the number, but it is much easier to explain logarithms in mathematical symbols rather than words.
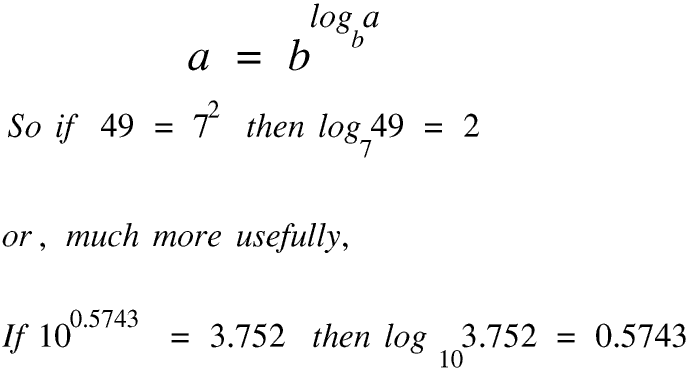
Logarithms to base 10 are called common logarithms: we usually miss out the base 10 when writing common logarithms. Your calculator has a log key and a 10x key so you can use them to check these numbers. (I looked up these numbers in a printed book of 4 figure tables, which was the standard way of working with logarithms and powers before calculators were around.) Almost all logarithms, to any base, are irrational numbers, so although I worked to four significant figures your calculator will display the answer to ten. Irrational numbers are explained on the Page on Natural and other numbers.
We can use any number greater than zero, except 1, as the base but for reasons which will become clear on the next Page, until the coming of the pocket scientific calculator people very rarely used any bases other than 10 and e (e is explained on Logarithms Page D). (A discussion about why the base must be greater than zero is beyond the scope of this Page.) Today logarithms to base e are called natural logarithms, although they were originally called Napierian logarithms. We write natural logarithms as ln.
The restriction that the base cannot be 1 is necessary because 1 to any power, even zero, is always 1. Also, we cannot have the logarithm of zero, to any base, as there is no number greater than zero which raised to any power gives the value zero.
Today the calculator has made working with bases other than 10 and e child’s play. We can show that
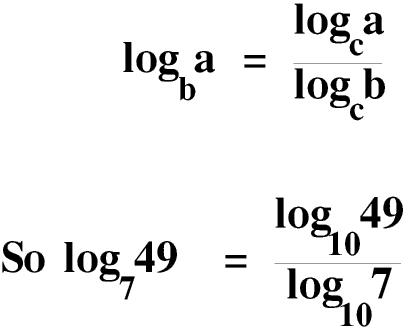
Although the right hand side is common logarithms I have left the 10 in the base to make it easier to understand. Use your calculator to prove that the answer is 2, as shown at the top of this Page, then use the same method to find the logarithm of 3.79 to the base 5.69. You should be able to do it in less than ten seconds. Before the pocket scientific calculator calculations of this sort would have taken even a very experienced mathematician several minutes, which is why only the most advanced mathematicians would have used anything but common and natural logarithms, and then only for the most specialised purposes.