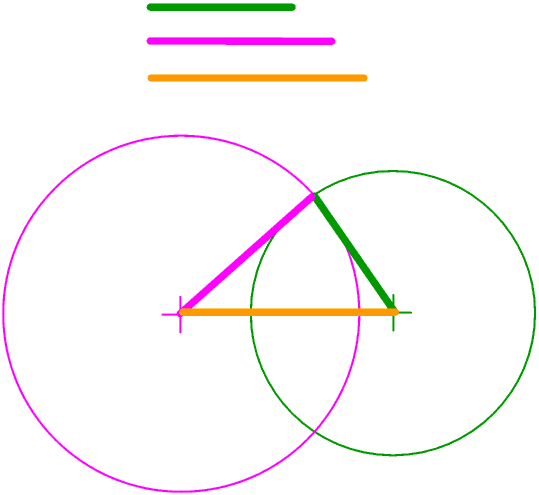
If we have three coloured rods which we want to join together to make a triangle, and we fasten one end of the green rod to one end of the brown rod, the other end of the green rod must lie on the green circle. Similarly if we fasten one end of the magenta rod to the other end of the brown rod, the other end of the magenta rod must lie on the magenta circle.
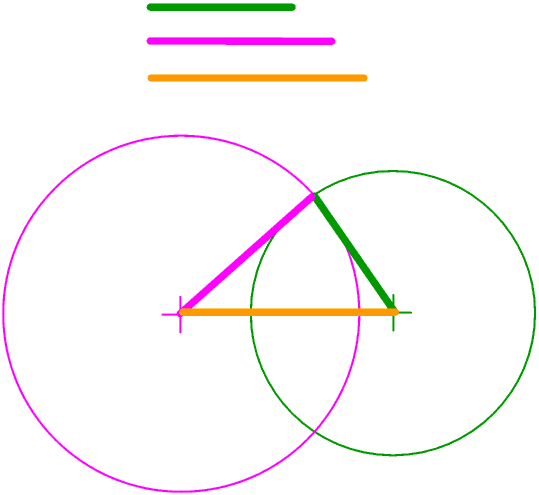
If however we add a fourth, dark grey, rod to make a quadrilateral there are three ways of joining the rods since any of the grey, magenta or green rods can be opposite the brown. In what follows we have shown the green rod opposite the brown.
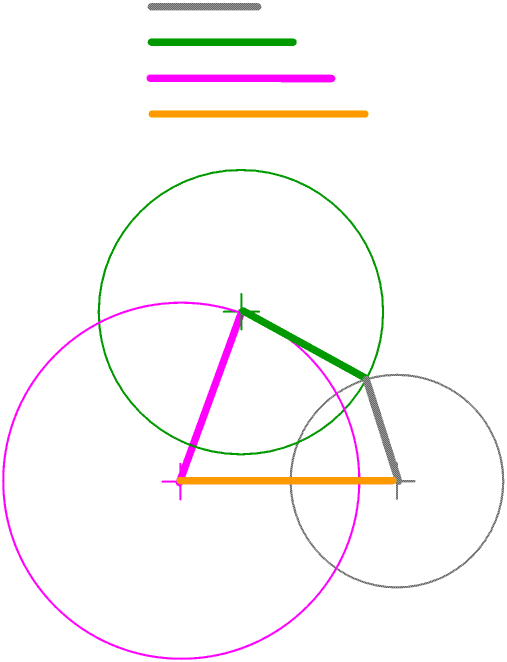
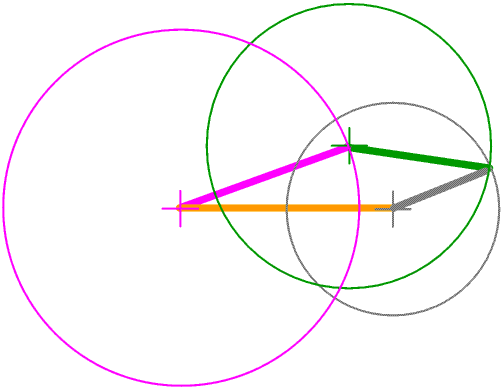
In fact four or more rods pinned together at their ends make what is called a mechanism. You can try this for yourself with Lego or Meccano or any other similar construction kit.

Of course, there are many more times when you want to join a number of rods in a way which does not form a mechanism, assembling a climbing frame for a small child for example. You can lock a quadrilateral into a particular shape by putting in a diagonal: this converts it into two triangles, and for a triangle once the length of the sides are fixed so are the angles.
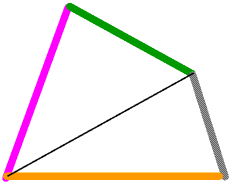
There are also other ways of using diagonals or cross-members to lock rods or poles into place.
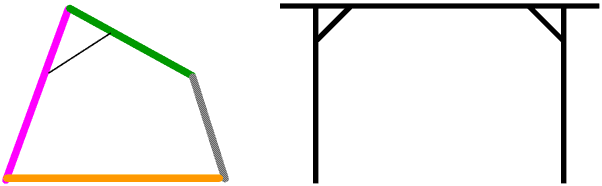
Next time you pass a building with scaffolding round it look to see if you can spot the cross-members which keep it all in shape.
All of this leads to one conclusion: even if we know all the sides of a quadrilateral, or any polygon except a triangle, we do not know anything at all about its shape.
Here we have a quadrilateral.
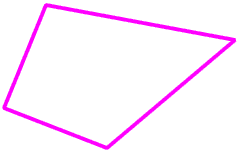
If we draw lines parallel to each of the sides we get other quadrilaterals with exactly the same angles but all totally different shapes and sizes.
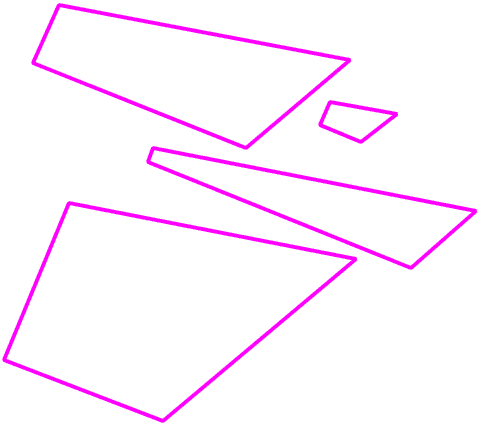
This leads us to another conclusion: even if we know all of the angles of a quadrilateral, or any polygon except a triangle, we still do not know anything at all about its shape.