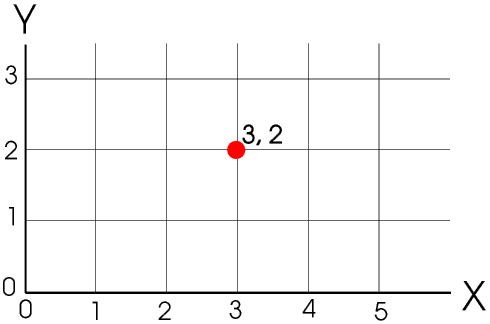
Trigonometry, polar and cartesian co-ordinates, and circular motion.

We can give the position of a point in two dimensions in one of two ways: we can use cartesian co-ordinates, x and y, or we can use polar co-ordinates, ρ (rho) and θ (theta).

Cartesian co-ordinates are named after the French mathematician René Descartes (1596 - 1650). The position of a point is given by its distance from the two axes (almost invariably called X and Y).

In polar co-ordinates the position of a point is given by its distance from the origin (ρ or rho) and the angle the line from the point to the origin makes with a horizontal line through the origin (θ or theta). The length of the line is always positive and (in mathematics) the angles are measured anti-clockwise. Polar co-ordinates

Compass bearings are usually measured clockwise from North but are not considered further here.

The relationship between the cartesian and polar co-ordinates of a point is given by

x = rho cos theta
y = rho sin theta
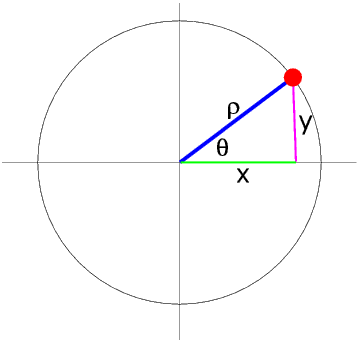
First Quadrant

We can see that sin theta = cos (90° - theta)

In the First Quadrant theta is in the range 0° to 90°. In the Second Quadrant theta is in the range 90° to 180°.

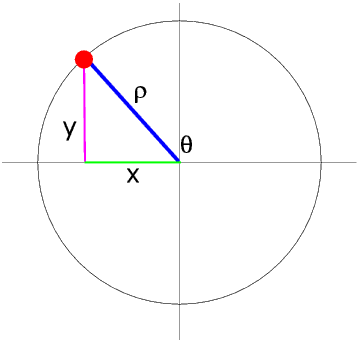
In the Second Quadrant y is still positive but x is negative so sin theta is positive but cos theta is negative.

We can see that sin theta = sin (180° - theta) and cos theta = - cos (180° - theta)

In the Third Quadrant theta is in the range 180° to 270°.

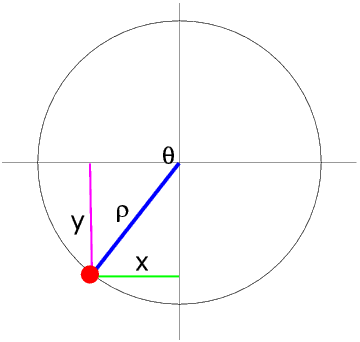
In the Third Quadrant both x and y, and so both sin theta and cos theta, are negative.

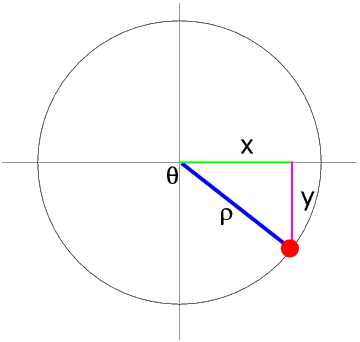
In the Fourth Quadrant theta is in the range 270° to 360°. Here y is negative but x is positive so sin theta is negative and cos theta is positive.

Here are curves of sin theta and cos theta for theta from -90° to +450°. The pattern is repeated every 360°, so sin (theta + 360°) = sin theta, cos (theta + 360°) = cos theta etc .

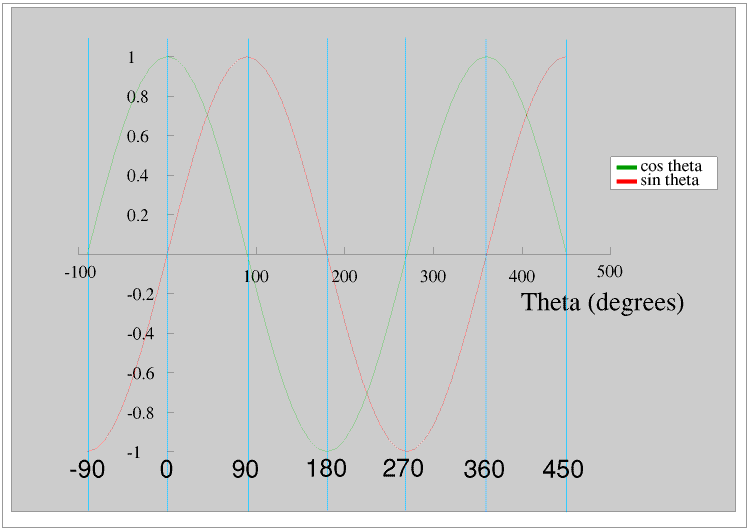
The graph covers values of theta from -90° to +450° to make it easier to see that although the sine and cosine curves have the same shape, called a sine wave, they are 90° apart (are 90° out of phase).

Although for each value of theta there is only one value of sin theta and one of cos theta, for each value of sin theta and cos theta there are two values of theta (more of course if you include angles less than 0° or greater than 360°), and this is important when we are using trigonometry to calculate the sides and angles of a triangle.