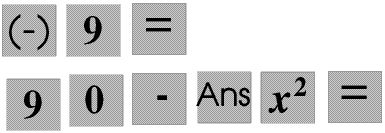Adding, subtracting and multiplying whole numbers or decimals is very straightforward: you just enter the sum exactly as it is and press =, for example
Initially you will be given the answer to this sum as a fraction, on some earlier Casio calculators as an improper fraction. This will not usually be what you want, and in most cases if you wrote this down as your answer it would actually be marked as wrong. To convert it to a decimal you just press the 
(Symbolic to Decimal or SD) key. Pressing the SD key again brings it back to an improper fraction. To turn it into a mixed number you use the shift function of the SD key, pressing the SD key again (without shift) brings it back to an improper fraction and so on.
Brackets come in pairs. With some calculators if you do not put in a closing bracket it will be put in for you at the end when you press =, but with others, including G4 calculators, it will flag an error, a syntax error. A syntax error means you have made a mistake in the way you have typed something in. (A maths error means you have tried to do something you are not allowed to do by the Rules of Maths, like dividing by zero.) It is best to get into the habit of always closing brackets, partly because your next calculator will not do it for you, but mainly because you might have left out a bracket in the middle of the sum by mistake, and putting it in at the end will change the sum. For example 3 × (2 + 5) - 8 × 7 + 3 is not the same as 3 × (2 + 5 - 8 × 7 + 3)
You can miss out the × sign if you can miss it out when you write the sum, for example 2(3x + 4) or (2 + 3)(4 + 5) or 3x² or 2π - but you do need to be careful with this if the calculation involves a division, see next Section.
If you give your calculator a sum where the answer is very big or very small it may give the answer in standard form.
Try 123456789 × 987654321 = or 0.000000123 × 0.000000987 =
Standard form is described on another Page; I mention it here only because if you are just starting at secondary school and this is your first scientific calculator you may not have come across it before.
You can enter several short calculations on a single line if you separate them by colons - you need to press the ALPHA key before the : of course. Try
2 + 3 : 3 + 5 : 6 + 7
When you press = you will get 5, press it again and you will get 8, press it again and you will get 13, press it again and you will get 5 again. When your calculator is displaying an intermediate result, that is the 5 or the 8, the word Disp appears in the top line of the display.
This is an incredibly useful feature and some of the ways you can use it to help you solve problems are described later, in the Page on Memories.
When we include division in our sums the situation is very slightly different because the answer may include a recurring decimal, and in Maths Mode we can use fractions.
To enter a fraction we use the fraction key 
When we press the fraction key a horizontal line (the vinculum) appears. We then enter the numerator above the line. When we have entered it we use the down cursor control key to move the cursor to the bottom of the fraction and enter the denominator, and then use the right cursor key to say that we have finished entering it. The cursor is now in the right place to continue entering the rest of the sum. The numerator and denominator can be simple numbers or expressions.
We can enter a mixed number by using the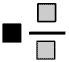 
key in the same way - we must press the shift key first of course
When working in One Line Mode rather than Maths Mode you just use the divide key, but remember if the top or bottom of the fraction are expressions rather than numbers you must use brackets, and there is one special case where you need to take care with this.
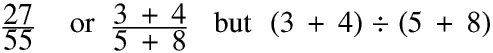
Find the radius of a circle with a circumference of 600 mm. Give your answer to the nearest millimetre.
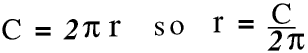
Putting in the numbers the radius is 95 mm. This is not a problem, ever.
However most people intuitively treat 2π as a number rather than an expression and so if we are not writing it as a fraction we would normally write it as C ÷ 2π, and this is the way some Casio and other calculators work, so if you enter this into it you will get the answer 95 mm. But according to the Strict Rules of Maths this should be
This situation arises because in the strict Rules of Maths multiplication and division are of equal rank, so if they are both present in a sequence of operators the calculation is done from left to right, whereas many calculators and many current PC applications treat an implied multiplication as of higher priority than ordinary multiplication and division.
Exponentiation however is of higher rank so 5 ÷ xy is (5 ÷ x) × y whereas 5 ÷ x² really is 5 ÷ (x²)
This divides the number by 100 (use the SHIFT key of course). Try
The SD key switches between a common fraction, a recurring decimal, and a decimal to ten significant figures.
If you fail to notice the dots you might think the answer is 0.54 but of course the correct answer is 0.55
You can enter recurring decimals by using the 
key. You press it (using the SHIFT key first of course), then the first number in the sequence. As you add the remaining numbers in the sequence the dots stay on the first and last, and when the sequence ends you use the right cursor control key.
Your calculator will give the answer as a common fraction, and this is probably the easiest way of converting a recurring decimal into a common fraction, but in an exam questions involving such conversions will usually be in the non-calculator paper so you do need to know how to do them without one, and this is explained on the Recurring Decimals Page.
The answer that you write in your book or on paper will not always be the answer that your calculator gives you. You will certainly be using your calculator in science and geography and many other subjects as well as maths, and this may affect the way you write your answer. This is further discussed on another Page.
In maths, but not usually other subjects, it may sometimes be correct to give your answer as a recurring decimal, proper fraction or mixed number, but it will almost never be correct to give it as an improper fraction.
A common fraction cannot have zero as the numerator, so two and a quarter and one and three quarters is four. But if you are working in decimals, in the same way that 2.24 + 1.74 = 3.98 so 2.25 + 1.75 = 4.00 but your calculator will give the answer 4 by itself.
On the other hand, although your calculator will often give you an answer to ten significant figures you should almost never write them all down. Sometimes you will be told how to give your answer, for example two places of decimals or three significant figures, but otherwise you must just be sensible.
There is more about this on another Page.
Finally, and this is probably the quickest way there is of losing marks in an exam, remember that if you are calculating the area of a shape where you have been given the length of the sides in metres, your calculator may say 65.37 but the correct answer is 65.37 m².We often need to do calculations involving negative numbers and your calculator can carry them out. Negative numbers are explained on another Page, this Section is specifically about using them on your calculator.
If we do the sum 5 − 9 the answer is a negative number. When I was at school we were taught that the answer was “minus four”, but if we really want to understand negative numbers it is more helpful if we refer to it as “negative four”, and today many people are teaching and using this term, and I shall use it on the rest of this Page and on other Pages.
If you are not very confident about using negative numbers on your calculator the simplest and safest way, and one which is never, and will never be, wrong is to put them in brackets, for example if we want the square of negative nine we write it, and enter it into our calculator as (-9)². Similarly 5 − (-2) and 6 × (-3). Your calculator will always give the right answer to these sums. If you are happy about doing this you can ignore the rest of this Section, but if you are serious about maths you will at some point need to come back to this Section.
It is important to stress that the rest of this Section is only about the way you enter negative numbers, not the way in which your calculator stores them and works with them.
We can write the sum three times two as 3 × 2 When we are handwriting or typing a sum like this it it is sometimes easier to understand if we put spaces before and after the ×, as I have, and this is not wrong, although we do not put them in when we enter the sum into our calculator.
In sums like this we are using +, −, × and ÷ as operators. We cannot normally have two operators together, for example try 7 + × 3. On all makes of scientific calculators this will bring up a syntax error message. Almost all basic calculators just use the last operator entered and ignore all the others, for example 3 × − ÷ + 4 = 7
But we also use + and - to show positive and negative numbers, for example +8 and -5. Here the + and - are not operators they are a part of the number and so we should not put a space between the + or - and the number. Mathematicians use slightly different symbols for these two different uses. There is a negative number key on almost all calculators. On the Casio fx-83 it is the 
key, but on other makes of calculator it might be labelled something different, for example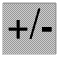 
. The design of this key on the Casio fx calculator reminds us of what it really does. In everything that follows (-) means press the key with this sign on it. On this calculator the negative number key makes a character slightly smaller than the ordinary minus key: try 
.
On some makes of calculator you must use the negative number key, so if you enter 8 − −6 you will get a syntax error, but on a Casio fx calculator you will not, you can always use either (-) or − to enter a negative number. It is however a good idea to get into the habit of using (-) because it helps you to understand the difference between − as an operator and - as the sign which forms a part of a negative number.
Note that on a Casio fx calculator you can use − instead of (-) but you cannot use (-) instead of −, if you enter 8 (-)6 this will be flagged as a syntax error.
We must of course always put in the - before a negative number, but we do not usually put in the + before a positive number unless there is a reason why we should.
Suppose we want to find the value of 90 − x² when x = -9 We would write this in our maths book as 90 − (-9)². We can always enter it into our calculator just like this, that is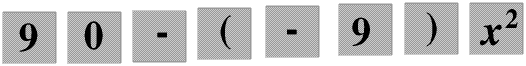 
and this will always give the right answer of 9, +9 that is. If you are ever uncertain about how to use your calculator with a negative number just put the number in brackets, this is never wrong.
If we choose not to put in the brackets and enter
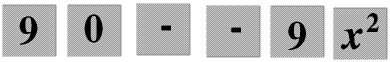
A Casio fx does the second, whether you use the − key or the (-) key. The instructions with the calculator explicitly tell you that if this is not what you want you must use brackets.
The moral of this is that unless you are totally familiar with the way your calculator treats negative numbers when you enter them in every possible situation you are safest just using brackets. If in doubt DIY.
It is important to emphasise that this Paragraph is only about the way you enter negative numbers not about the way the calculator handles them internally once you have entered them. If for example you enter
