
Positive and Negative Numbers
When we are doing sums we often use the symbols +, − × and ÷ to tell us what sum to do. These are operators. For example 2 × 3 + 7 would tell us to multiply 2 by 3 to make 6 and then add 7 to 6 to make 13. We normally talk about adding, subtracting, multiplying and dividing although in Early Years Teaching we sometimes use take away instead of subtract.
Similarly 7 − 4 means subtract 4 from 7 to make 3, and 4 − 7 means subtract 7 from 4 to get -3. When I was at school we were taught to call this “minus three” and many older people still do, but it is easier to understand negative numbers if we call it “negative three”.
We do however still talk about a temperature of -3°C as minus three - we should always write °C but we do not always say it.
The negative number sign in front of the three is not an operator it is a part of the number, and it is unhelpful to call it a minus sign. In most printed books slightly different symbols are used for the subtract and negative number signs, but this is not always well explained at school, and it is difficult to use different symbols when you are handwriting, so when handwriting it is best to put a space after a subtract sign so there can be no doubt that you are using it as an operator. But there is a negative number sign key on most scientific calculators, for example on a Casio fx-86 calculator the negative number sign key is  . Try
. Try  on your calculator and you will see the difference. The answer is 13, +13 (positive thirteen) but we do not normally put in or say the positive sign unless there are special reasons why we should (there sometimes are), and your calculator never does. On other makes of calculator the negative number key may be something like
on your calculator and you will see the difference. The answer is 13, +13 (positive thirteen) but we do not normally put in or say the positive sign unless there are special reasons why we should (there sometimes are), and your calculator never does. On other makes of calculator the negative number key may be something like 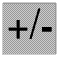 .
.
Using negative numbers on your calculator is more fully explained on another Page.
Key to understanding negative numbers is the Number Line. Number lines are widely used by little children, and older students are sometimes scared to use them because they think they are only for babies - but this is silly.
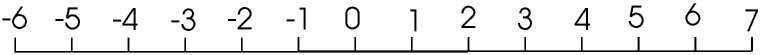
The numbers get larger as we move to the right and smaller as we move to the left, so 5 is bigger than 3 and, just as importantly, -3 is bigger than -5.
Adding and subtracting negative numbers
When we are adding numbers we move along the number line to the right. If we are doing the sum 2 + 3 we start at 2 on the number line and then move 3 to the right so end up on the 5, so 2 + 3 = 5. Similarly if we are doing -2 + 3 we start on -2 and move 3 to the right so end up on 1, so -2 + 3 = 1.
When we are subtracting we move along the number line to the left, so if we are doing 6 - 2 we start on the 6 and move 2 to the left and so end up on 4. Similarly 3 - 5 is -2 and -2 - 4 is -6.
If we are doing 4 + -1 we start on 4 and move -1 to the right (that is +1 to the left) so end up on 3, so 4 + -1 is 3, and similarly 6 + -4 is 2 and -4 + -1 is -5.
If we are doing the sum 4 − -2 we start on the 4 and move -2 to the left, that is +2 to the right, so end up on the 6, so 4 − -2 = 6. Similarly 3 − -3 is 6 and -5 − -6 is 1
In effect, 3 + -2 is the same as 3 − 2 and 3 − -2 is the same as 3 + 2. This is sometimes explained as “Two negatives make a positive” but I do not think this helps us to understand what is happening.
Multiplying and dividing negative numbers
If we are multiplying 2 × 3, we start at 2 and multiply our distance from zero by 3, so end up on 6. Similarly -2 × 2 is -4. If we are multiplying by a negative number we move in the opposite direction, so 3 × -2 is -6 and -2 × -2 is +4.
Similarly for division. -6 ÷ 2 is -3 and -4 ÷ -2 is +2 Rounding negative numbers
When we are rounding numbers, for example to the nearest whole number, if the number to be rounded is exactly half way between two whole numbers we always round up, so 6.3 will round to 6, 4.7 will round to 5 and 3.5 will round up to 4. Similarly -3.2 will round to -3, -2.9 will round to -3 and -5.5 will round up to -5 rather than down to -6.
© Barry Gray March 2016
 . Try
. Try  on your calculator and you will see the difference. The answer is 13, +13 (positive thirteen) but we do not normally put in or say the positive sign unless there are special reasons why we should (there sometimes are), and your calculator never does. On other makes of calculator the negative number key may be something like
on your calculator and you will see the difference. The answer is 13, +13 (positive thirteen) but we do not normally put in or say the positive sign unless there are special reasons why we should (there sometimes are), and your calculator never does. On other makes of calculator the negative number key may be something like 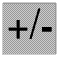 .
.