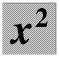To square a number you just enter the number and then use the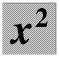 
key. If you are squaring an expression you must put it in brackets. You can square any number. Try 5², 6.7², 0², (3.97 ÷ 2.79)² and (-4)². You must put negative numbers in brackets; remember that the square of a negative number is always positive.
To find the square root of a number you press the square root key and then enter the number or expression. In Maths Mode a straight line (a vinculum) appears over the numbers as you enter them, and you tell your calculator you have finished entering the number or expression by using the right hand cursor control key, in One Line Mode there is no vinculum so the number or expression must be inside brackets.
Try √(81), √(3), √(16.81 + 15.19) and √(1.92) - the way the answer is displayed may not be quite what you expect! It is explained next, just use the SD key to get the answer as a decimal.
Most square (and other) roots are irrational numbers. Irrational numbers cannot be expressed exactly as a fraction or decimal so once you have used the SD key your calculator will give you the answer to ten figure accuracy. Irrational Numbers are explained in greater detail on the Page on Natural and Other Numbers.
To ten figure acuracy the square root of 2 is 1.414213562, but you can of course express it to twenty or even five million figures. Stating the obvious, the exact value of the square root of two is the square root of two. Try (√2)² and then try squaring 1.414213562 by entering all ten digits. In most cases, if your calculator can give you the exact answer to a sum then it will, even if this is not quite what you want. Square roots are called surds, and so, in Maths Mode, your calculator will often give you an answer containing surds. (Originally a surd was any root, but today it is almost invariably used only for square roots.)
If we square a negative number we get a positive number, for example try (-3)², so there is no real number which when squared gives a negative number, that is, the square root of a negative number cannot be a real number. The square root of a negative number forms part of a complex number. Complex numbers are explained on another Page.
The Casio fx cannot handle complex numbers, so if you try to find the square root of a negative number you will get a maths error: try √(-4). There are calculators which can handle complex numbers (I have one), but if you have one and know how to use it you will probably not be reading this Page; if you have one and do not know how to use it you have probably bought or been given the wrong calculator...
π is the ratio of the circumference to the diameter of a circle, and it also crops up in nature and mathematics in the oddest places. It is an irrational number, its approximate value, to 0.1% accuracy, is 22 ÷ 7, or to ten figures 3.141592654. There is a π key on your calculator.
π is mentioned here because your calculator deals with π in the same way as it deals with surds. The exact value of π is of course π so if your calculator can give the exact answer to a sum involving π then it will: try π × 5²
Surds and π are the only irrational numbers treated in this way, all other irrational numbers (including the result of calculations involving both surds and π) are given only as a decimal to ten figure accuracy.
Most calculators have keys for cubes and cube roots, and they are entered in exactly the same way as squares and square roots. Most cube and other roots are irrational numbers and are given to ten figure accuracy - only square roots are displayed exactly, as surds.
To calculate, say, 
we use the 
key, that is, we press 5, then the key, then 4 followed by the right hand cursor control key.
To calculate, say, 
we press the 
key (use shift of course) then 4 followed by the cursor control key, then 128 followed by the cursor control key.
Remember that in most cases if a key has an x on it we enter the number and then press the key, whereas if it doesn’t we press the key first and then enter the number. This fits in with how we say what we are doing: we say “five to the power of four” but “the fourth root of five”.
We can in fact raise any number to any power or take any root of any number (with a very few exceptions, all involving zero). Such calculations are now routine in most school work on radioactive decay, but even thirty years ago would have been quite beyond all school students.
You can use negative and fractional powers and roots of positive and negative numbers without really understanding them, just remember
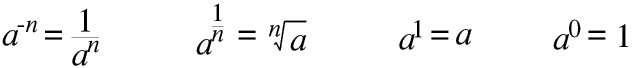
but if you do want to understand them you might like to visit the Powers page.
Remember that the answer may often be irrational or part of a complex number. (If you get a syntax error it is because you have pressed the wrong key.)
There are just a very few exceptions. a0 = 1 and 0a = 0 for all values of a except zero, but 00 is what mathematicians call undefined: try it for yourself and you should get a maths error.
Similarly a ÷ 0 is undefined, for all values of a including zero, so we shall get a maths error if we try 5(1÷0) and therefore also the zeroth root of any number.
The reciprocal of a number is found by dividing 1 by the number, for example the reciprocal of 2 is 0.5 and the reciprocal of 0.5 is 2, while the reciprocal of 2/3 is 3/2. Reciprocals are very useful in many areas.
You can of course always find the reciprocal of, say, 5.3 by entering 1 ÷ 5.3, or even 5.3-1, but most calculators have a dedicated reciprocal key, in this case x-1,where you just enter the number and then press the key.
There are six other keys associated with powers but these are not considered here. The ×10x key is discussed on the next Page under Standard Form, and the two log keys and the ln key and the powers of 10 and powers ofe keys are discussed on the Logarithms Page.
