We often find it useful to write numbers such as 3 × 3 as 3². We say this as three to the power of two, or more usually three squared.
In the same way we can write 7 × 7× 7 as 7³. We say this as seven to the power of three or more usually seven cubed. Similarly 5 × 5 × 5 × 5 is 54 or five to the power of four.
We can in fact raise any number to any power, for example 8 × 8 × 8 × 8 × 8 × 8 × 8 × 8 × 8 is 89 or eight to the power of nine.
If you are about eleven years old or younger you can stop here, you do not need to know anything else about powers. But this very simple way of writing numbers leads us into a completely new branch of mathematics. In what follows each Section builds on the one before so you can stop at any time, when you have got as far as you need, but you can also go straight to any Section.
Correctly we call the power to which a number is raised the index, although an older term, exponent, is still often used, for example in exponential decay - exponential decay is explained on another Page.
If you have a scientific pocket calculator - and most of what follows on this Page assumes that you have - you can use powers (and square roots and other roots and logarithms, all of which depend upon powers) without knowing anything else about them, but I think you will find powers, and in fact all maths, much more interesting and a lot easier to understand and remember if you take the time and trouble to find out a little more about them.
Using powers on the type of Casio calculator commonly used in English schools is explained fully on the Powers and Calculators Page. Other makes and models may have slightly different different labels or be used in slightly different ways but the result will be the same, just try the examples I give out for yourself to make certain you understand how to use your calculator.
If 44 is 4 × 4 × 4 × 4,
and 46 is 4 × 4 × 4 × 4 × 4 × 4,
then 44 × 46 is 4 × 4 × 4 × 4 × 4 × 4 × 4 × 4 × 4 × 4
or 44 × 46 = 4(4 + 6) or 410
Similarly if we write 53 × 58 out in full we can show that it is 5(3 + 8) or 511
This leads us to our First Rule. In algebraic notationThis is “obvious” if a, m and n are all integers and equal to or bigger than 2.
We show later on this Page that it is true even if a, m and n are not integers or not greater than or equal to 2: the only restriction is that a is not zero (though m and n can be), and this is implicit, even if it is not made explicit, in everything that follows on the rest of this Page.
We can show that
This leads us to a corollary of our First Rule
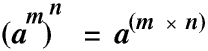

It is easy for us to visualise what is meant by, for example 56, or even our First Rule am × an = a(m + n) if we think of a, m and n as integers bigger than 2. But many people find it difficult to visualise, for example, what is meant by 50 or 6-3 or even 2.371.52 in the same way. But even if we cannot visualise them they are still real numbers, with real values (1, 0.00463 and 3.712 if you want to know), because we made the Rule that 2 × 2 × 2 should be 23 and this is where the Rule we made leads us. If you have any problems with understanding this it might be helpful for you to look at the Page on Natural Numbers where it is explained in greater detail.
If 7× 3 is 21 and 7 × x is 21 this is only possible if x = 3
So if a × b = c and a × d = c then b must be equal to d (unless a = 0)
Therefore 0m = 0 for all values of m except m = 0 and a0 = 1 for all values of a except a = 0 - try them on your calculator.
The value of 00 is what mathematicians call “undefined” and if you try it on your calculator you will get a maths error.

We can show, by writing out the sum in full, that
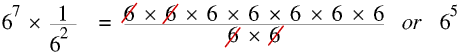
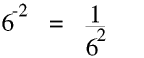
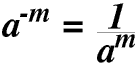 Unless a = 0
Unless a = 0
To follow the rest of this Page you must have a scientific pocket calculator with you, right now. If you haven’t, go away and get one, and while you are gone I will make a cup of tea.
Welcome back. If you are under thirty you will not remember the World before scientific pocket calculators, but it was a Very Different Place.
Computers, PCs and laptops have changed our lives, and the lives of almost all people living on this planet, in very many ways, but if you read through the next Sections you will realise that it is the scientific pocket calculator rather than the computer which has changed the way in which maths is taught in our schools and the way it is used in our everyday lives.For the rest of this Page “calculator” means a pocket scientific calculator.
Calculators have changed the way maths is taught and used because of their ability to do calculations involving irrational numbers. Irrational numbers are numbers which cannot be expressed exactly in the form a ÷ b and rational numbers are numbers which can be. Most square roots and other roots, trigonometrical functions such as sines and cosines, logarithms and of course π are all irrational numbers. Irrational numbers are discussed at much greater length on the Page on Natural and other numbers.
Today’s scientific pocket calculators make working with irrational numbers child’s play (literally), but thirty years ago working with irrational numbers was very difficult and time-consuming, and usually involved using printed books of mathematical tables, and only the most able students were taught to use them.Most (scientific) calculators less than three years old can work in Maths Mode or One Line Mode. In Maths Mode roots and powers (and also fractions and some other functions, but these are not considered here) are displayed exactly as they would be in your maths book, for example
In One Line Mode the sum is displayed all on one line, so powers and roots are displayed in a slightly different way.
This looks a little strange at first but you soon get used to it. You should try to become familiar with both modes.
To change from one mode to another you you use the SHIFT key followed by the SETUP key. This gives you a menu with a number of options. Press 1 for Maths Mode or 2 for One Line Mode. (There are also other modes, for example to allow you to choose whether to measure angles in degrees or radians.) Then you can use whichever mode you feel most comfortable with or which most suits the type of work you are doing.

Putting all the above Rules together we have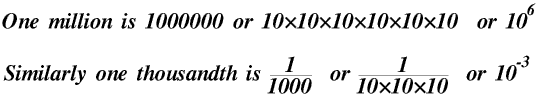
Here are all the powers of 10 from +5 to -6
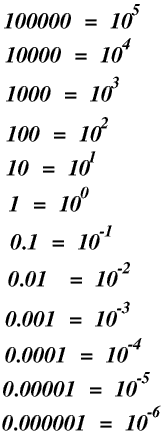
Numbers bigger than a million or less than a millionth may have rather a lot of zeros. This makes them tedious and time-consuming to write, and they also take up a lot of space on the page when they are written or printed. It is also very easy to get the number of zeros wrong: if you miss out or put in a zero you make the number ten times bigger or smaller. We can get round all of these problems by using powers of 10.
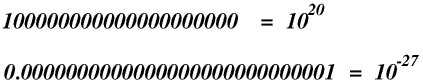
Mathematicians usually write very big or very small numbers in standard form. A number written in standard form has just one digit (1 to 9) before the decimal point, and a power of ten.
Examples of standard form
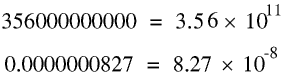
When converting a number to standard form the power of 10 is the number of times you must move the decimal point to make just one digit in front of it.
If you give your calculator a sum such as 1234567 × 7654321 where it cannot display the answer in full in the normal way it will automatically give the answer in standard form - try it for yourself. (A non-scientific calculator will do one of several things, depending on its make - but none of them will be to give the right answer.) You can also set your calculator so that it displays answers in standard form all the time (until you change it back), and of course you can always enter numbers in either standard form or in the ordinary way - make certain you know how to do all of these.
Scientists usually prefer to work with units based on thousands, for example watts, kilowatts, megawatts, gigawatts and terawatts etc, or seconds, milliseconds, microseconds and nanoseconds etc. Scientific form is similar to standard form, except that only powers of ten which are multiples of 3 are used, and the number before the decimal point is in the range 1 to 999.![]()
However not all scientists use scientific form all the time so you may see the speed of light given as 3 × 108 m/s or 300 × 106 m/s, and either would be regarded as correct. Most calculators give you the option of working in standard or scientific form.

Why this Section is included here will become apparent in the next Section.
If three squared is nine then the square root of nine is three. We use a special symbol for square and other roots: it was originally a modified letter r, for root.
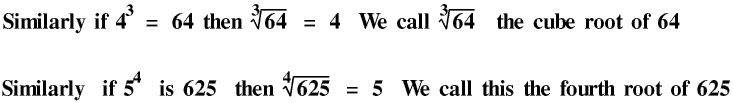
This is our Fifth Rule. It is true for all values of a and b except zero. The restriction that b is not zero is necessary because as any number (except zero) to the power of zero is 1 there is no way in which we can know what number was raised to the power of zero to give the answer 1! a and b can be negative but for reasons explained in the next Section your calculator cannot always cope if they are so this Section is only about positive values of a and b.
If 32 = 3 × 3 then 3.12 = 3.1 × 3.1 Today most people (most people who know their times tables that is!) know that 32 is 9 and can work out the value of 3.12 quite quickly with pencil and paper.
Similarly if 175 = 17 × 17 × 17 × 17 × 17 then 17.675 = 17.67 × 17.67 × 17.67 × 17.67 × 17.67
Working this out without a calculator is straightforward long multiplication but will need pencil and paper and take most people several minutes. (Or you could use logarithms - logarithms are discussed in another Section, below.) But with your calculator you can work out this, or in fact any number to any power, in a few seconds.
Most people can see that every number has a square, but it is not always apparent to everyone that every positive number also has a real square root. But it is quite easy to prove. For example, 1.97² is 3.8809 and 1.98² is 3.9204, so if we draw a number line there is one point, just one point but still a real point, such that the square of every number to the left of it is less than 3.90 and the square of every number to the right of it is more than 3.90. So this point is the square root of 3.90, whatever scale we use for our number line.
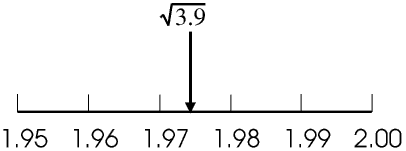
Of course, proving that it exists and actually calculating its value are two different things.
Here are the calculations needed to find the square root of 3.9 to four significant figures.
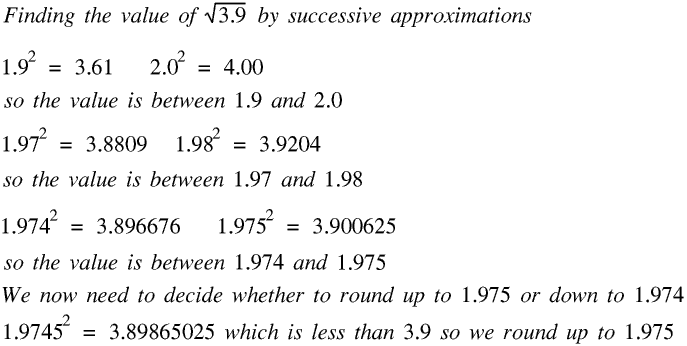
You could of course calculate the 13th root of 76.545 to 4 decimal places in exactly the same way, provided you rent a quiet cottage in the country for a week or so and remember to turn your mobile phone off.
I have included this example to show how the pocket calculator has revolutionised calculations involving square and other roots, and in fact all irrational numbers: a calculation which thirty years ago would have taken a very experienced mathematician at least a quarter of an hour, or several days, can now be done by anyone at all in less than five seconds, and to ten rather than four figure accuracy. Today the distinction between rational and irrational numbers is for most people of no practical significance at all.

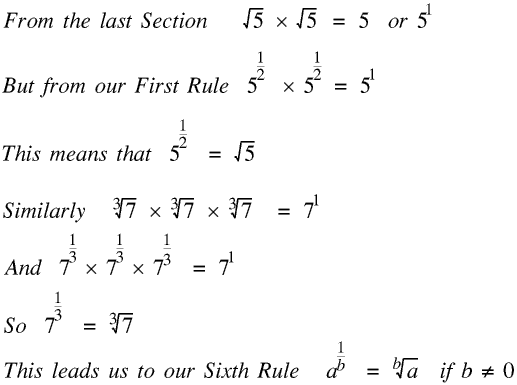
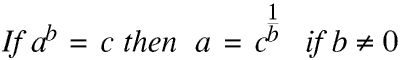
But I put in the Section on Roots before this because I think this makes it easier to understand.
Putting all the above Rules together we have
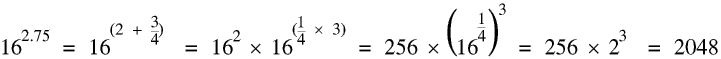
Of course you could do it on your calculator rather more quickly.
What this means is that we can raise any positive number to any power, so for example 7.748-6.398 has a real value, although most numbers to non-integer powers will be irrational.

Logarithms are so important they have their own Page, but they are a special type of power which is why they also have a section on this Powers Page.
Logarithms were invented by the Scottish mathematician John Napier (1550 - 1617). The logarithm of a number to any base is the power we must raise the base to in order to get the number, but it is much easier to explain logarithms in mathematical symbols rather than words.
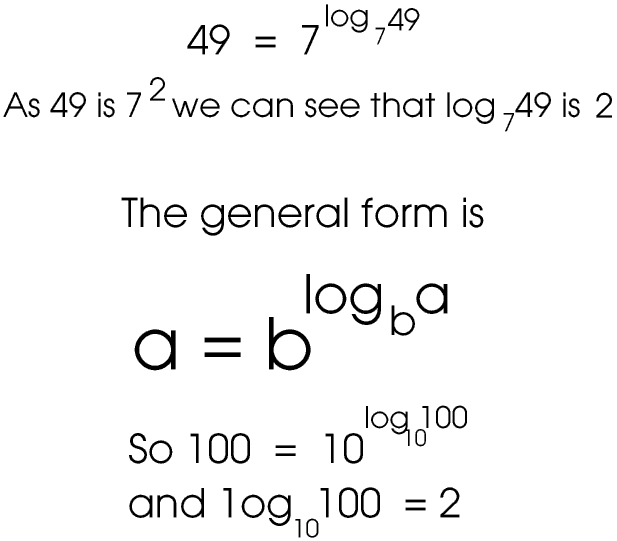
Almost all logarithms are irrational numbers. We can use any positive number (except 1, and of course 0) as the base but for reasons given on the Logarithms Page we usually only use common logarithms (base 10) and natural logarithms (base e). Natural logarithms are given the symbol ln and are explained fully on the Logarithms Page; we usually omit the base 10 from common logarithms. Your calculator should have both a log key and a ln key (and a 10x and ex key).
Try log 5.768 on your calculator. To 4 significant figures it is 0.7610 This means that 5.768 = 100.7610
Now try log 2.347 - this means that 2.347 = 100.3705
What this means is that 5.768 ÷ 2.347 = 10(0.7610 - 0.3705) or 100.3905 which is, using the 10x key on your calculator, 2.458.
Of course, you could do the calculation on your calculator in two or three seconds, but until about forty years ago, before pocket calculators, it would have taken you five or six minutes. By using logarithms we have changed a division into a subtraction, which is much quicker. But of course you would not have had a calculator to find the logs, so you would have had to look them up in a book, and the whole operation would still have taken one or two minutes. As I said, it is the pocket scientific calculator which has revolutionised the way maths is taught and used.
This is, or rather was, one use of logarithms, but they have many other uses, even in this calculator age, which are explained on their own Page.
