Man has been marking out circles on the ground for nearly ten thousand years. The best way to draw a large circle on the ground is to take a piece of rope and fix the ends to a point in the ground so as to leave a loop, then put a lump of chalk or ochre or anything else that will leave a mark on the ground into the loop, then walk round, keeping the rope taut.

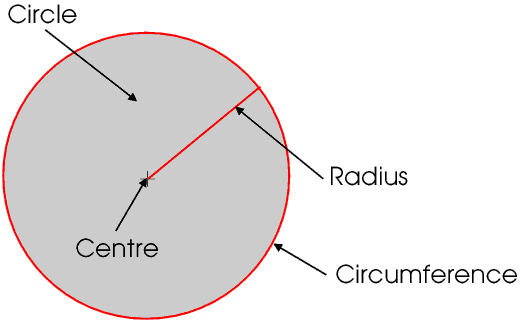
The point where we pin the ends is called the centre of the circle, and the line drawn by the chalk or ochre is called the circumference. Any straight line drawn from the centre to the circumference is called a radius (plural radii.) Because of the way we drew the circle all radii are the same length.
If we pin the ends of the rope to different points we draw not a circle but an ellipse. The pin points are called the foci (singular focus). The Earth and all the other planets go round the Sun in ellipses with the Sun at one focus, not in the middle. This is discussed further on one of the Astronomy Pages of my Web Site.
Today if we are drawing a circle on a piece of paper we usually use a pair of compasses. We usually mark the centre with a small cross before we draw it so we can see where it is - finding the centre of a circle after we have drawn it is not easy!
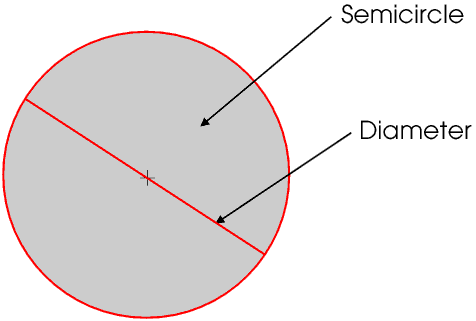
A straight line across a circle and passing through the centre is called a diameter. A diameter divides the circle into two equal semicircles.
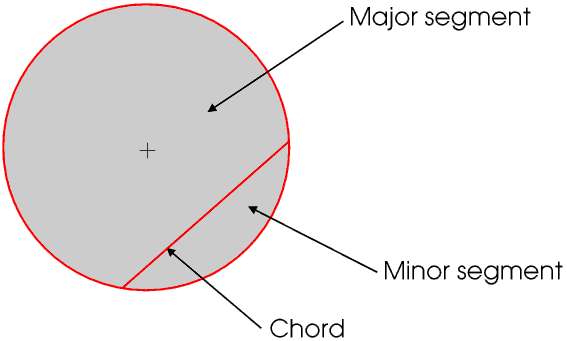
A straight line across a circle but not passing through the centre is called a chord. A chord divides the circle into two unequal segments. These are correctly called the major and minor segments (from the Latin for greater and lesser), although we usually refer to a minor segment as just a segment.
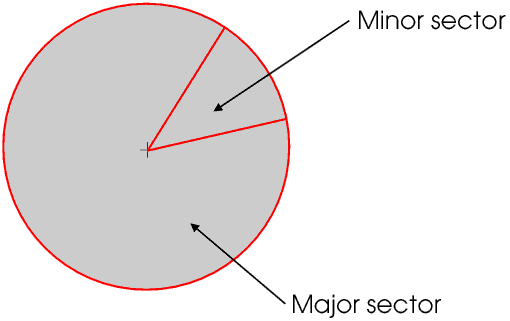
Two radii divide the circle into major and minor sectors, although we usually refer to a minor sector as just a sector.
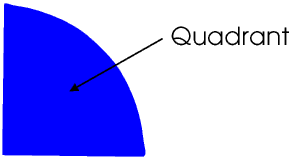
A quarter of a circle, that is, a minor sector with an angle at the centre of the circle of 90°, is called a quadrant.
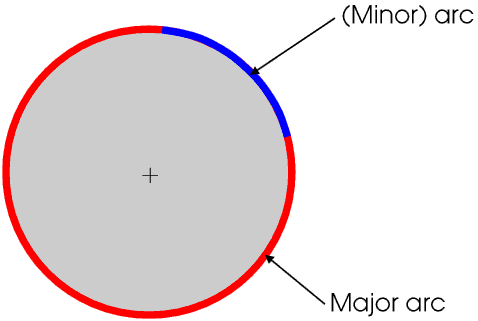
A part of the circumference of a circle is called an arc.
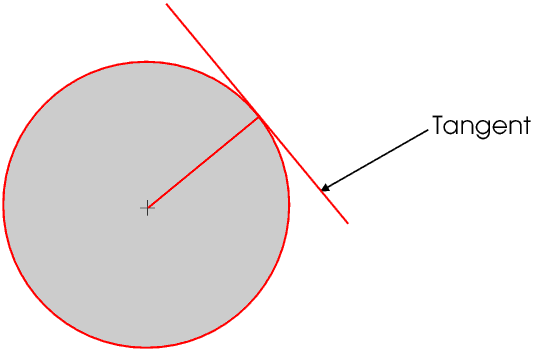
If a straight line just touches the circumference at one point but does not cross it it is a tangent (from the Latin tangeo meaning I touch). The radius to the point is a normal to the tangent, that is, it is at right angles to it.
The circumference of a circle is a little more than three times the diameter, whatever the diameter of the circle. The exact value of the ratio is given the Greek symbol π (pronounced and often written pi). π is what is called an irrational number, a number that cannot be expressed exactly as a common fraction. To eight decimal places π = 3.14159265. Irrational numbers are described on another Page. Most scientific calculators have a π key; if you are using a basic calculator (without a π key) or even not using a calculator at all you will probably not need eight figure accuracy and 22 ÷ 7 will give you the value of π correct to three decimal places, which will probably be accurate enough. Many web sites give you more accurate values of π; one gives it to a million decimal places! The actual value to any required accuracy can be calculated from the formula
but only with a powerful computer or several months shut up in a cottage in the country. There are actually several different formulae for π which at first sight do not look much like each other, but they all give exactly the same value. π keeps cropping up in Nature and in mathematics in the oddest places.
If C is the circumference of a circle, A its area, r its radius and d its diameter,We are so used to measuring angles in degrees that we often lose sight of the fact that degrees are entirely Man-made. The first people to divide a circle into 360 parts (degrees) were the Ancient Babylonians, nearly five thousand years ago. They chose 360 because it is 60 × 6, and 60 can be divided into 2, 3, 4, 5, 6, 10 and 12 parts.
The ruins of Babylon are in present-day Iraq.In the same way that for a circle the ratio of the circumference of a circle to its radius does not depend upon the size of the circle, so neither for a sector does the ratio of the arc to the radius depend upon the size of the circle.
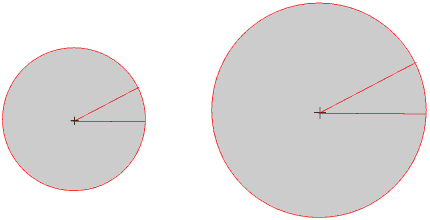
But the ratio does of course depend on the size of the angle: if you keep the radius constant but double the angle you double the arc and so double the ratio of the arc to the radius.
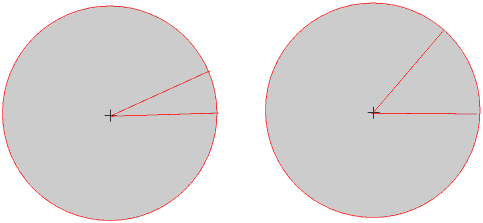
The size of an angle, in radians (rad), is the ratio of the arc to the radius, and is found by dividing the arc by the radius. In some branches of mathematics we usually give angles in degrees, but in other branches we must use radians. The radian is the only official SI unit of angular measurement.
The circumference of a circle is 2πr so turning all the way round in a circle is 2π radians. So 360° is 2π radians, and π radians = 180°. Therefore to convert from degrees to radians you multiply by π and divide by 180; to convert from radians to degrees you multiply by 180 and divide by π. So a radian is about 57.296°.
We usually give fractions of a radian in decimal format, for example 1.36 rad; we can give fractions of a degree as a decimal, for example 73.68° or in minutes and seconds, for example 54° 37' 44". (There are sixty seconds in a minute and sixty minutes in a degree.) Your scientific calculator has a function key which allows you to choose whether to work in radians or degrees, and you should make sure you know how to use it.
If a line is not horizontal you can also give its slope or gradient - these are described on another Page.