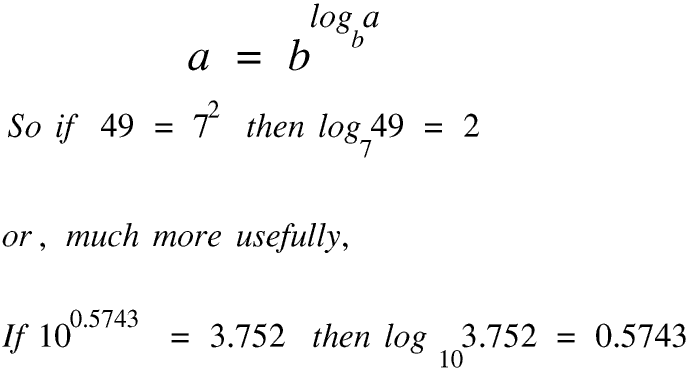
Recapping from the first Page on logarithms.
Logarithms were invented by the Scottish mathematician John Napier (1550 - 1617). The logarithm of a number to any base is the power we must raise the base to in order to get the number, but it is much easier to explain logarithms in mathematical symbols rather than words.
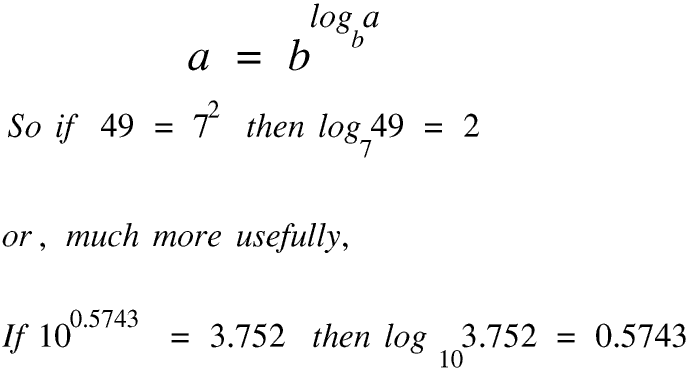
Logarithms to base 10 are called common logarithms: we usually miss out the base 10 when using common logarithms. Your calculator has a log key and a 10x key so you can use them to check these numbers. (I looked up these numbers in an old printed book of 4 figure log tables, which was the standard way of working with logarithms before calculators were around.) Almost all logarithms, to any base, are irrational numbers, so although I worked to four significant figures your calculator will display the answer to ten. Irrational numbers are explained on the Page on Natural and other numbers.
Four hundred years ago, when logarithms were invented, most people, in Britain and everywhere else, lived in villages and worked on the land. These people did not need to be able to do any mathematics except the most simple sums. But some groups of people, architects, navigators on sailing ships out of sight of land, astronomers, have always needed to be able to do more than this. Working out the slope of the sides of a square based pyramid with smooth equilateral triangle sides requires considerable mathematical skill, and when an Ancient Egyptian Pharaoh called Sneferu built the first such pyramid he was less than a quarter of a degree out - four thousand five hundred years ago!
We get out our 4 figure log tables and find that log 2.763 is 0.4414 and log 3.512 is 0.5456 (If you don’t have a set of 4 figure log tables you may use the log key on your pocket calculator.)
This means that 2.763 × 3.512 is 100.4414 × 100.5456 or 10(0.4414 + 0.5456) or 100.9870We get out our inverse log tables (originally called antilog tables) and find that 100.9870 is 9.705 (If you do not have a set of inverse log tables you may use the 10x key on your calculator.) Check the answer by doing the multiplication on your calculator if you like, but remember that because we were using four-figure tables there may be rounding errors in the fourth decimal place.
Most people used four figure tables but five, six and even seven figure tables have been published. Four figure tables give the logs for 2.763, 2.764, 2.765, 2.766 etc, but seven figure tables give the logs for 2.763186, 2.763187, 2.763188 etc so by the time you have included all the numbers from 1.000001 to 9.999999, and of course another set of tables for the inverse logs, they are rather too bulky for you to do your homework on the school bus. (Why you need to cover only numbers between 1 and 10 is explained later on this Page.)
It is possible to do the calculation by long multiplication although it is very time-consuming, but until the invention of logarithms there was no other way. By using logs we have changed a long multiplication into an addition, which is much quicker. Nothing like as quick as using your calculator, but still a great step forward for 17th century astronomers, navigators and architects. If we go back another two hundred years we still need to use long multiplication, except that now (in Europe) we are using Roman numerals and common (ordinary) fractions not decimals.
Of course, calculating the logs of 2.763 and 3.512 is much much more difficult and time-consuming than just doing the long multiplication, so for people to use logs in this way someone else must already have done it. For people to be able to use his logarithms Napier could not just invent them, he also had to calculate their values and publish a set of log tables as well. And this is why until the coming of the pocket scientific calculator most people did not use anything other than common and natural logarithms: no one had published log tables for any other bases!
He did however only need to calculate the values of the logarithms for numbers between 1 and 10. This is because we can write any other number in standard form, for exampleWe can use common logarithms to calculate the values of powers and roots in a similar way.
