This Page is one of several Pages about nuclear science. This Page is about half-life; other Pages deal with the structure of the atom, radioactivity, ionizing radiation and health and safety, the uses of radioactivity, carbon and other forms of dating, nuclear fission and nuclear fusion.
This Page assumes you are familiar with the structure of the atom and radioactivity, and in particular understand the meaning of the words isotope and nuclide. If you are not you might like to read the Pages on these first.Doctor, Doctor, shall I die?Everyone alive today is going to die, although we do not know when. But we can predict very accurately how many people aged 70 today will still be alive in ten years time.
Yes my child, and so shall I.
In the same way, if we have a certain number of atoms of a radioactive substance, say bismuth-210, we cannot predict when any particular atom will disintegrate. But we can predict very accurately how many will have disintegrated in an hour. The key to understanding the rate of decay of a radioactive substance is half-life. The half-life of a radionuclide is the time taken for half the atoms in a sample, any sample, to decay. The half-life of bismuth-210 is about 5 days, so if we start with 200 g of bismuth-210 today, in five days time we shall have only 100 g. But what is special about half life, for all radionuclides, is that it does not depend upon the amount of the substance we start with. So after another five days we shall only have 50 g of bismuth-210; after another five days we shall have only 25 g.
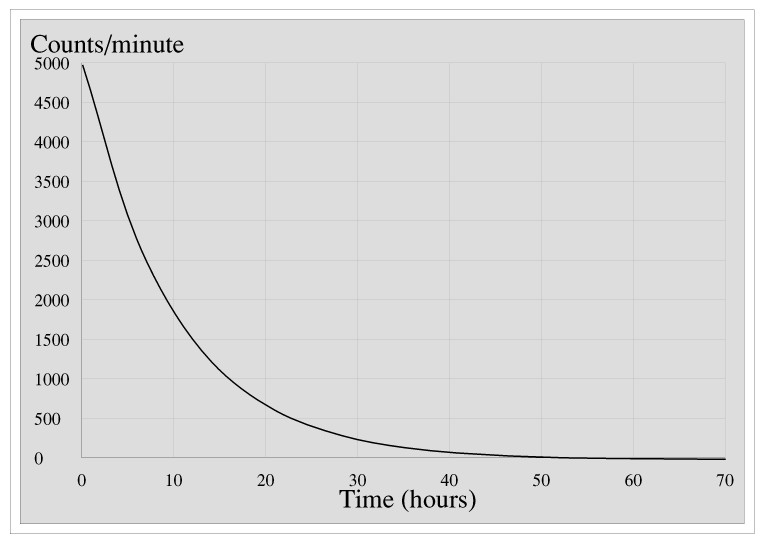
Thomas, Richard and Henry do some experiments on a sealed source of a certain radionuclide to determine its half-life. They measure the activity of the source, in counts per minute, every hour for three days. Here is a graph of their results.
To find the half-life they choose any value of the counts per minute, say 4000, and read off the time, here about 2 hours, and then do the same for half the number. The time taken for the rate to drop to 2000 counts per minute is about 9 hours, a difference of 7 hours, so the half life is 7 hours. The best way to understand half-life is to try this for yourself by printing the graph and using it to measure the time for the count rate to drop from, say, 2000 to 1000, or 1500 to 750: assuming I (or rather my spread-sheet package) have drawn the graph accurately the answer should be 7 hours whatever value of count rate you start with. This is the nice thing about half-life.
As described on the Radioactivity Page of my Web Site, half-lives for radionuclides vary from 2 × 1015 years for neodymium-144 (this is a hundred thousand times the age of the Universe from the Big Bang!) to 125 nanoseconds for astatine-213 (a nanosecond is a thousand millionth of a second!), and everything in between. So radioactivity decay calculations often involve very big or very small numbers. The Science Pages of my Web Site are not designed to help you become a nuclear physicist but are intended only to help young people to understand scientific ideas well enough to cope with school-leaving exams, and to enable all my Readers, young and old, to take an intelligent, well-informed and useful part in debates on scientific issues. For this reason I have chosen only very simple examples, involving only either whole numbers of half-lives or graphical solutions. Real-life situations are of course nothing like so simple and the calculations needed are quite complex, but unless you are studying nuclear physics beyond school leaving age you will probably never encounter them. If you are interested in the calculations you can find an easy to follow explanation on this web site - you need to scroll down on it to get to the section you want..
Please do not ask me how they measured the half-life of neodymium-144 or astatine-213!
Worked Example 1
A radioactive source is measured at 4064 counts per minute, but 105 minutes later the count has dropped to 127. What is the half-life of the source?
First we multiply 127 by 2 as many times as we need to to get 4064. 127, 254, 508, 1016, 2032, 4064. We have multiplied it by 2 five times, so 105 minutes represents 5 half-lives so the half-life is 105 ÷ 5 or 21 minutes. We could also divide 4064 by 127 to get 32, and then work out that 32 is equal to 25, but the first way is probably easier.
After n half-lives the activity of a source has dropped to
of its initial value. So after 10 half-lives the activity, of any radionuclide, has dropped to less than 0.1% of its original value. We normally assume that a source has ceased to be radioactive after ten half-lives - mind you that is almost fifty thousand million years for radionuclides such as uranium-238! For carbon-14 ten half-lives is only 57 300 years, so carbon dating cannot be used to determine the age of anything more than about 50 000 years old.The carbon in the carbon dioxide in the atmosphere is about 99% carbon-12 and 1% carbon-13, with about one part in a trillion (1012) of carbon-14. Carbon-14 is radioactive, with a half-life of 5730 years. All food chains begin with a plant taking in carbon dioxide for photosynthesis so all living things contain minute amounts of carbon-14. Once the organism dies the carbon-14 in it decays (radioactively - not to be confused with biological decomposition) and so the ratio of carbon-12 to carbon-14 in it changes with time. By measuring this change we can determine when the organism died. There is much more about this on the Carbon dating page of my Web Site.
An archaeologist wants to date a bead necklace found in a cave used by mesolithic Man. She cannot of course use carbon dating to find the age of the beads because they are not made from organic matter, but she can use it to date the remains of the leather cord. She burns a tiny piece of the leather in pure oxygen, and this converts the carbon in it into carbon dioxide. She separates the carbon dioxide from all the other gases, and then reduces the carbon dioxide back into pure carbon. She finds that 0.095 g of this carbon has a radioactivity of 1.45 counts per minute. She works out that 1 g of this carbon would give 1.45 ÷ 0.095 or 15.26 counts per minute. She knows that 1 g of carbon from modern organic sources gives 122.08 counts per minute. 122.08 ÷ 15.26 = 8, which is 23, so the bead necklace is 3 half-lives, or 3 × 5730 or 17 190 years old.Of course many objects that we want to carbon-date are less than 5000 years old, less than one half-life, so the calculations are not so easy. Also remember that we are trying to measure the change in the ratio of carbon-12 to carbon-14, when our starting point is a ratio of carbon-12 to carbon-14 of about a trillion to one!
The first people to use radiocarbon dating, in the 1940s, used a value of about 5600 years for the half-life of carbon-14, and you may still find this figure used in some books, including science text books.
