Almost all cars and boats and aircraft, cameras, tablets and smartphones, and many other things, are now fitted with satellite navigation systems which give you your position to an accuracy of better than five metres, almost anywhere in the world. Satellite navigation systems use the Global Positioning System (GPS). This Page is about how the GPS works.
“Until the development of global positioning systems triangulation was the only practical method of measuring distances for map-making” (Quote)
What nonsense - but it has been repeated so often and in so many books and web sites that everybody seems to believe it! But triangulation (trigonometry) remains right at the heart of the Global Positioning System.
Lots of words in maths and science come from Latin or Greek words. (Lots more come from Arabic, Indian or Persian.) A plane figure with straight line sides is called a polygon, from the Greek for many sides. We call an eight-sided figure an octagon, from the Greek for eight sides, a six sided figure a hexagon, and a five sided figure a pentagon. We could call a four-sided figure a tetragon, from the Greek for four sides, but we usually call it a quadrilateral, from the Latin for four lengths. (But we do call a solid with four faces, such as a triangular based pyramid, a tetrahedron, from the Greek for four faces.) Similarly we could call a three-sided figure a trigon, from the Greek for three sides, but we usually call it a triangle, from the Latin for three corners. But the trigon in trigonometry comes from the Greek for three-sided, so trigonometry (from the Greek) and triangulation (from the Latin) just mean measuring with triangles.
Trigonometry is about triangles. When we draw a triangle we usually use capital letters for the angles and small letters for the length of the sides, where the side with length a faces angle A.
If we have a triangle with angles A, B and C and sides a, b and c and then draw another triangle, keeping the angles the same but doubling the length of just one side we also double the length of the other two sides, that is, the ratio of the lengths of the sides remains the same. In any triangle the ratio of the lengths of the sides depends only on the angles, and the angles depend only on the ratio of the lengths of the sides. This is always true of all triangles; it is never true of any other polygon. There is more about this on the Page on The Shape of a Polygon.
This means that for any triangle we can calculate all the sides and all the angles if we know or are given
![]() three sides, or
three sides, or
![]() two sides and one angle, or
two sides and one angle, or
![]() one side and two angles.
one side and two angles.
All we need to do the calculations are the trigonometric functions of sine and cosine.
If we are given three angles but no sides we can draw lots of triangles all of different sizes, but they will all be the same shape. Triangles of the same shape but different sizes are said to be similar.
In order to draw an accurate map we need to know the position of all the hills, villages, rivers, woods, fields, churches, castles etc to be shown on it, and this means knowing the distances between them.
Today if we need to know the distance between two points, say a church and a castle, we just go to the church, point our “laser tape measure” at the castle and press a button, and there is the answer, to the nearest centimetre (provided we remembered to put in a battery). But in the days before laser tape measures almost the only way to measure a distance of more than a couple of metres directly was to use a real tape measure or a trundle wheel, or to pace it out (as the Romans did: our word mile comes from the Latin mille passuum which means a thousand paces, except that a Roman pace was what we would call a double pace), and this was not easy if the castle and church were about eight kilometres apart, each on the top of a (different) hill, and in between them there was a river, a village, a wood, and a field with a bull in it.
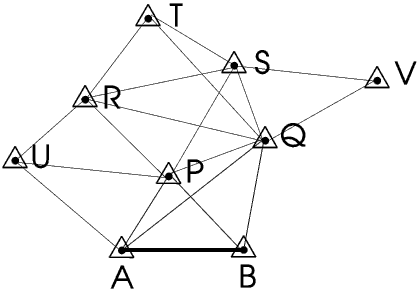
This is where trigonometry comes in. First we find a place, away from villages, rivers, woods and fields with bulls in them and where the ground is quite level, and then set up a Base Line. We measure the length of this as accurately as we can, and set up a trig (trigonometry or triangulation) point at each end. A trig point is a special marker which can easily be seen from a long way away. On larger-scale British Ordnance Survey maps trig points are shown as a triangle with a dot in the middle. It is a criminal offence to damage or in any way disturb a trig point.

Then we set up other trig points. These can be on the tops of hills, on church towers, almost anywhere where they can easily be seen from a long way away.
Measuring the bearings of trig point P from A can be done very easily and very accurately with a special telescope on a tripod called a theodolite.

We can measure the bearing of P from B in the same way.
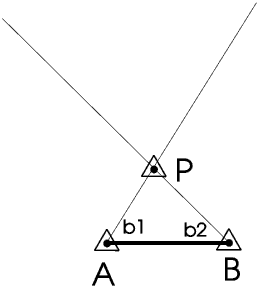
Once we know the bearings of P from A and from B, point P is where the two lines cross. This fixes the position of P. Then we can use the trigonometric functions to calculate the distance of P from A and B. We have put trig points at the ends of our Base Line so we can double-check our measurements by taking back-bearings of A and B from P - if we can see P from A and B then we can see A and B from P.
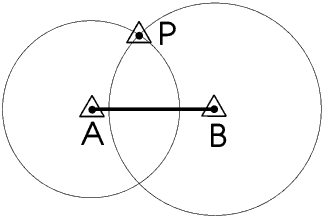
Fixing a point by making a triangle in this way is called triangulation.Of course if we know the distance of P from A and B rather than the bearing we can fix P in a similar way, by drawing one circle centre A and radius AP and another centre B and radius BP, then P is where the two circles meet. This of course is how we triangulate using the Global Positioning System - this is described later but I mention it here to emphasise that the GPS is as dependent upon triangulation as any of the methods of navigation and map-making which came before it. The circles intersect at two points but I do not think there can be any doubt about which of them is point P!
We can fix the position of trig point Q in the same way.
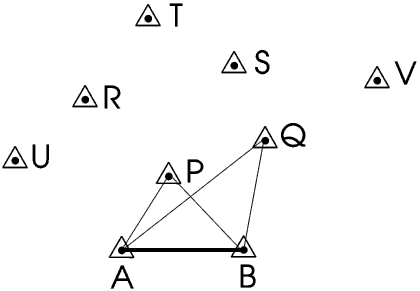
Having fixed P and Q we can use them to fix trig point R, and then S and T, and so on until we have mapped the whole country.
The original Base Line for the Ordnance Survey was about seven kilometres long and was set up in 1784 in West London on what was then Hounslow Heath - you can still see the two half-buried cannons which marked the beginning and the end, and you can read more about it by clicking here ![]()
You can of course triangulate across water in this way provided you can see across, for example the English Channel. One of the first uses of triangulation from the original Ordnance Survey Base Line was to measure the distance between what were then the two finest observatories in the world, in Greenwich and Paris, because astronomers thought that knowing this distance really accurately would help them to improve the almanacs (printed tables giving the positions of the Sun, Moon, planets and stars at different places and times, and also details of eclipses of the Sun and Moon) which navigators were using to find their position on long sea voyages out of sight of land. There is more about almanacs and navigation, and how Christopher Columbus's almanac saved his life in one of his voyages to the Americas, in the last two Sections of my Page on Eclipses, although you have to read the whole of these two Sections to understand why I think they might be helpful in a Page on navigation.
Triangulation in map making and navigation had of course been used for thousands of years before that, the Ancient Greeks had measured the distance of the horizon, and from that worked out the diameter of the Earth, using triangulation more than two thousand years ago.Trigonometry has been used for thousands of years, right back to the building of the Egyptian Pyramids, and ought to be really exciting and interesting and relevant to the world around us. But the tragedy is that almost everything that is interesting, exciting and relevant about trigonometry has been taken out of the way it is taught in Schools, and what is left is often taught in a way which young people find boring and irrelevant to the real world.
The Ancient Egyptians were very great mathematicians, scientists and engineers. They first started building huge pyramids out of blocks of stone nearly five thousand years ago.
Most people, when they want to show what brilliant engineers and mathematicians the Ancient Egyptians were, choose to talk about the Great Pyramid at Giza, built by a Pharaoh called Khufu. But I think the finest example of their use of trigonometry is a pyramid built fifty years earlier, by Khufu’s father, a Pharaoh called Sneferu, who reigned from 2575 to 2551 (BCE of course!)
All the Pharaohs before Sneferu had built their pyramids as a series of steps. Sneferu started building a square based step pyramid but then decided to convert it into a true pyramid, with smooth equilateral triangular sides. This didn’t work very well - the sides fell off! Today it looks like a step pyramid surrounded by a pile of rubble.
So he built a second pyramid, and this time he started it as a true pyramid. We can use trigonometry to show that the slope of the sides of a square-based pyramid with equilateral triangle sides should be 54 degrees 44 minutes. The slope of the sides of Sneferu’s second pyramid, the first ever built as a true pyramid, is 54 degrees 27 minutes - just one quarter of a degree out!
Unfortunately when it was half-finished the foundations started to crumble and they had to reduce the slope to save weight so that it didn’t collapse completely - the builders were probably very conscious of what had happened to their Master’s first pyramid! Today we call it the Bent Pyramid. It is the best preserved of all pyramids, but it is not on what might be called “The Official Ancient Egypt Tourist Trail” so not a lot of people visit it or know about it. You can see some pictures of the Bent Pyramid on the Bent Pyramid Web Site.
Sneferu went on to build a third pyramid and this was completed OK.To build a pyramid this accurately you need to be able to triangulate in three dimensions. You can fix a point in three dimensions by triangulating from any three points not in a straight line. Of course the more points we have to triangulate from the more accurate the result: Sneferu could triangulate from the four corners of his square base.
The Global Positioning System was originally developed by the United States Government for military use, and at first they tried very hard to stop other people from using it, but eventually they gave up and now anyone can use it for free, all you need to do is to buy a GPS receiver.
The GPS consists of twenty four GPS satellites each orbiting the Earth twice a day at a height of about 20 000 kilometres in a very precise orbit.
Each of the GPS satellites and every GPS receiver contains a clock, and all of these clocks are set to exactly the same time. Each GPS satellite broadcasts this time continuously, and also an almanac, saying exactly where it is supposed to be at that time. This signal travels at the speed of light, which means that by the time it reaches your GPS receiver there will be a difference between this time and the time given by the clock inside the receiver. This time difference enables us to calculate the distance between the GPS satellite and the GPS receiver - to an accuracy of less than a metre!
Each GPS satellite checks its position and the accuracy of its clock at regular intervals from signals from a ground control station; each GPS receiver sets its clock for the first time from special signals received from the GPS satellites as they pass overhead: this process can take up to an hour because you need to receive signals from at least four different satellites, but need usually only be done once; once the time has been set it is automatically checked every few hours, a process taking only a few seconds.
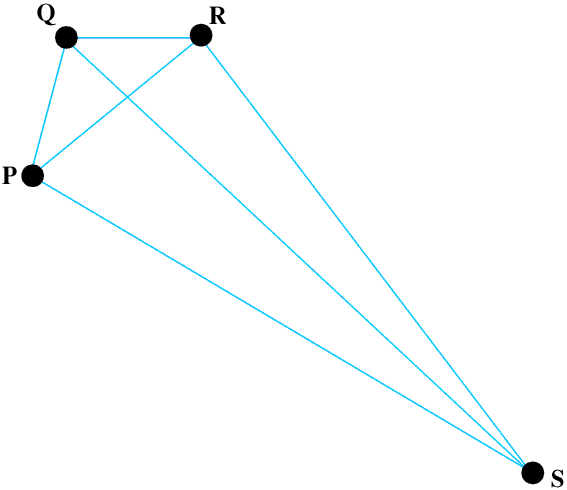
We have three points P, Q and R, not in a straight line. We know their positions in three dimensions. If we know the distance of another point S from P, Q and R we can use trigonometry to fix the position of S in three dimensions.
In a Global Positioning System P, Q and R are GPS satellites travelling though space at about 15 000 km/hour about 20 000 km above the Earth, and S could be a man walking across Dartmoor, or it could be a military aircraft flying along a valley in the Scottish mountains at 600 km/hour and a height of 25 metres above the ground, or it could be a point near the crater of a volcano in South America! So don’t let anyone tell you that the GPS has replaced trigonometry, for map-making, navigation or anything else - trigonometry is still at the heart of GPS, it is just that because the calculations need to be done rather more quickly and accurately than you can do them on your pocket calculator people think of GPS as magic and forget that the mathematics involved is as old as the Pyramids....In theory to fix your position you need to be receiving signals from only three GPS satellites, but as there are twenty four of these circling the Earth you will normally be receiving signals from five or six (some GPS displays tell you how many), and this will give you your position to an accuracy of better than five metres, in three dimensions. This is fine if you are delivering pizzas because you know which house you are outside, but not if you are in a car you are not actually driving because you do not know which side of the road you are on! Coverage is less complete in the extreme polar regions but even at the North and South Poles you will always be receiving signals from a minimum of three satellites which will fix your position to about a hundred metres.
The European Union has recently launched the first of the satellites for its own global positioning system. This uses much more modern technology and will eventually lead to a system giving positions to an accuracy of better than ten centimetres. This accuracy might not be of great importance to you if you are the navigator on a Cruise Ship (unless you forgot whether you put your Cabin Key into your left-hand or right-hand pocket), but knowing that a point near the crater of a volcano has moved six centimetres in six days might be a matter of life and death to the people living near it.
The GPS gives you, or rather allows you to find, your position, nothing else. Satnav systems which show your position on a map and give spoken directions to your destination use additional software and hardware - it is the type and quality of this software and hardware which determines the size and weight, and of course cost, of your satnav system.
The GPS is rather like a large sheet of plain white paper: what you use it for is limited only by your own imagination.
The GPS allows you to find your position in three dimensions, nothing else, but you can use this information in many different ways.
For thousands of years many explorers and travellers have kept journals, and some of these, for example Marco Polo's journey from Venice to China and back again with his father and uncle from 1271 to 1295, still make fascinating reading. Today's explorers and travelers could include their GPS co-ordinates in their diaries each day to make them more interesting (or perhaps not, perhaps just more useful).
Many photographers use a camera with a built-in GPS receiver which automatically records the position from which each photograph was taken, while many people use the GPS in their smartphones to find their way to the nearest (insert your own favourite please).
We can use GPS to locate and track almost anything: an armoured truck carrying gold bullion, a blind man (wearing a GPS receiver) chasing a remotely controlled model car with a bell (and a GPS receiver) inside it all over a large open space (useful in studies of how well blind people can follow sounds over distances of more than thirty metres), a bull elephant in an African National Park, a glacier moving a few metres a year, an iceberg drifting in the South Atlantic Ocean, or a beacon on a seismic fault line. When we are using the GPS in this way we need to transmit the information back to us in some way. It could be over a telephone line, mobile phone or radio link, it could even be a satellite link but of course the satellite would be a different, communications, satellite not a GPS satellite.
We can use the GPS to allow an airship to remain in a fixed position (on station) for days or weeks at a time - this is described on the Page on Airships in the 21st century, or to direct a rescue party to a climbing accident.
The use of the GPS has revolutionised almost every aspect of geology and other branches of science, and of course map-making and navigation. It is however in the area of navigation that most of the abuses of the GPS occur.
Big aircraft and big ships have lots of navigation aids on board, including very specialised, sophisticated and of course expensive GPS hardware and software, and also people who know how to use them. The trouble begins when we put satnave systems costing less than £100 and bought off the shelf in a supermarket into HGVs, Land Rovers, small boats, aircraft, even back-packs, driven, controlled, piloted or carried by people with no understanding of how they work or how to use them (use them sensibly that is). To some people they just are a Magic Box, rather like a Fairy Godmother: she always comes at once when you call her, she never needs to sleep or eat or drink, she is never ill or bad-tempered, she just smiles and waves her wand and makes everything better no matter what sort of mess you have got yourself into.
A satnav system does not require us to turn our brains off before we can use it, but almost every week we hear about HGVs crashing into bridges because their drivers listened to the instructions from their satnav systems and forgot to watch for or even just plain ignored “Low Bridge” signs. This sort of mistake is not usually life-threatening; to fly across an unfamiliar mountain area in a light aircraft, or cross a desert in a Land Rover, or sail out of sight of land in a cabin cruiser, or walk by yourself in a wilderness area with no radio, with no knowledge of navigation and no compass or maps or charts, most certainly is. But put a satnav system into your aircraft or car or boat or back-pack or a smartphone into your pocket and suddenly all of these become almost commonplace. Then not evenyour Fairy Godmother can save you if your satnav has a flat battery and you are a long way from the nearest mobile phone mast ....