This Page assumes you have read Pages A, B and C on logarithms, if you have not please do so now.
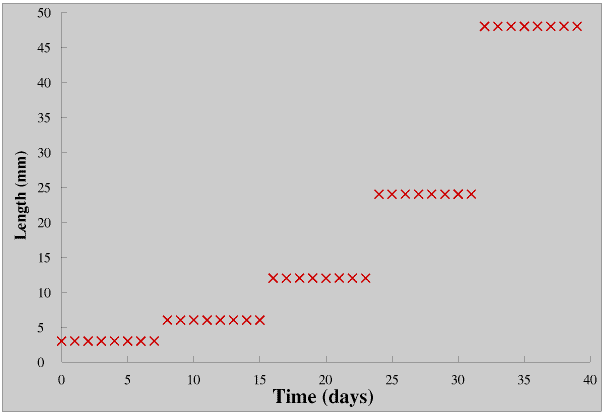
Albus goes to the same school as his brother James but he is a year younger so he is studying a caterpillar. He measures the length of his caterpillar every day for forty days. He plots his results.

He realises it is doubling its size every eight days from the day that it hatches from an egg (on Day 0) until it becomes a chrysalis (on Day 40). But he cannot understand why his results are not a smooth curve like his brother's.
His teacher explains that caterpillars and lots of other animals do not have bony skeletons inside them as we do, and also other vertebrates (mammals, birds, reptiles, amphibians and fishes), instead they have a very hard outer skin like a suit of armour, an exoskeleton. This has joints in it which allows the animal to move, but once it had hardened it does not grow, so the caterpillar can only get bigger by shedding its skin. When the caterpillar first hatches from the egg its skin is very soft and floppy and elastic, like an uninflated balloon. It sucks in air and blows itself up like a balloon and, like a balloon, it gets much bigger and its skin gets stretched tight and the caterpillar becomes quite rigid. Then its skin starts to harden, and after a short time its skin is quite hard. (Rigid and hard by caterpillar standards of course not by ours - but our skeleton is not very rigid or hard by the standards of a rhinoceros!) It is now twice as long, and twice as wide, and twice as high, as it was, and so its volume is 2 × 2 × 2 or eight times as big, so it is like a chocolate honeycomb sweet, more than 80% air bubbles! It starts to feed, and grows not by getting bigger but by expanding into the empty air bubbles inside its skin. Eventually it has filled all this space, so it sheds its old skin and the whole process is repeated. It sheds its skin several times before eventually it turns into a chrysalis and then a butterfly.While its new skin is hardening it is very vulnerable to predators (it cannot run away or protect itself from animals which might eat it) so it usually hides in a dark place just before it sheds its skin - this is why Albus never sees it happen.
Both James's plant and Albus's caterpillar are growing exponentially but one is growing continuously and the other in separate stages. The best way to understand the difference between these two types of exponential growth is to use an example from the world of money.
When James is born his parents Harry and Ginny invest in some special Bonds for Children. These double their value after sixteen years, about when James will leave School, but if you cash them in before sixteen years you only get your money back, you do not get any interest. Harry buys £10 000 of these bonds for James. He works it out that £10 000 added after sixteen years is equivalent to £10 000 ÷ 16 or £625 a year on £10 000, or 6.25% a year - we call this the AER or Annual Equivalent Rate.
If he were to leave the money in for another fixed period of 16 years (he’s not going to do so of course) it would double again, so it is growing exponentially.
When Albus is born Harry and Ginny wonder whether buying Bonds like this for him is the best they can do; it’s too late to change their mind about James. They sit down and do some sums.
Suppose, they think, the rate of interest stayed the same, at 6.25% a year, but the interest was paid in two instalments, at the end of eight and sixteen years.
The interest on £10 000 after eight years would be £10 000 × 6.25 × 8 ÷ 100 or £5000. So the total after eight years is £15 000 so over the next eight years interest will be paid on £15 000 not just £10 000. The interest for the next eight years will be £15 000 × 6.25 × 8 ÷ 100 or £7500, so the total at the end of sixteen years will be £15 000 + £7500 or £22 500. So the total has gone up by a factor of 2.25 not 2.
Now suppose the interest were paid every 4 years (adding the interest in 4 instalments). The first instalment would be paid after 4 years and would be £10 000 × 6.25 × 4 ÷ 100 or £2500 so the total after 4 years would be £12 500 and the interest for the next 4 years would be calculated on this amount. We can show that the total after 16 years would be £24 414, so the total has increased by a factor of about 2.44.
If the interest were paid every 2 years, in 8 instalments, the total after 16 years would be £25 658, so it has increased by a factor of about 2.57, and if it were added every year, in 16 instalments, the factor would be about 2.64 .We can show if the interest is paid every 6 months, in 32 instalments, the factor would be about 2.68, and so on.
We can plot the factor against the number of interest instalments - the graph is much easier to understand if we use a logarithmic scale for the number of instalments.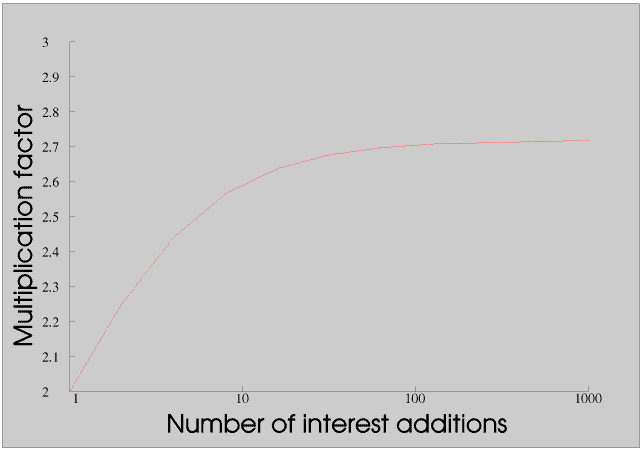
Its value to ten decimal places is 2.7182818283, but of course you can give it to any accuracy you like - even more than a million decimal places. You can find its value on your calculator (but not to a million decimal places!) by entering e1. Irrational numbers are explained in the Page on Natural and Other Numbers.
Most Banks and Building Societies calculate interest on a daily basis. Harry and Ginny realise that although they would get a lot more money by putting their money into a Building Society for 16 years at 6.25% they would probably not find any Building Society which offers them such a high rate of interest fixed for sixteen years. So they do what they should have done a year ago, and talk things over with their Financial Adviser.
But they have not totally wasted their time doing all these sums, they have rediscovered e!
e was discovered by Napier and is the base for natural logarithms. Natural logarithms were originally called Napierian logarithms and are the key to most calculations on exponential growth and decay - this is discussed in the next Page on logarithms, Page E.