Mathematicians call a shape drawn on a large flat surface such as a table-top (or better, if you do not want to get into trouble, a large piece of paper placed flat on a table-top) a plane figure or a plane shape.
Just to confuse things, geographers call a large flat area of land a plain, so we have the Great Plains of the United States.
If all the edges (sides) of a plane shape are straight lines it is a straight line shape, or a polygon, from the Greek for many sides. (But we often use polygon to mean only shapes with five or more sides.) The smallest number of sides a polygon can have is three. This is a triangle, from the Latin for three corners - in any polygon the number of angles is always the same as the number of sides. The “points” of a polygon are called its vertices (singular vertex).
This List gives the names of some other polygons.
Triangle and quadrilateral (from the Latin for four sides) come from Latin, but all the other names come from Greek. You will get a lot of Brownie Points for knowing the names of nine- and eleven-sided polygons! The Greek for a three-sided shape would be a trigon (hence our word trigonometry, meaning measuring with triangles) and for a four-sided shape would be a tetragon (which is why a three dimensional shape with four plane faces, that is, a triangular based pyramid, is called a tetrahedron).
Some people get muddled up between Latin and Greek, so call a heptagon a septagon and an enneagon a nonagon, but most mathematicians would regard this as incorrect.
There is more about trigonometry on another Page of my Web Site and to link to it please click here.
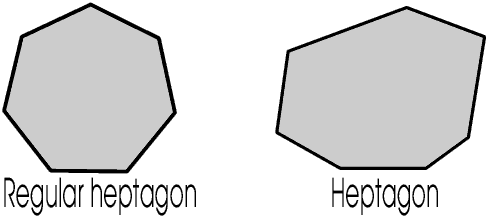
A regular polygon has all its sides and all its angles equal. If all the sides of a triangle are equal then all the angles must be equal, so an equilateral triangle is regular, but this is not true of any other polygon, for example in a rhombus all the sides are equal but all the angles are not, whereas in a rectangle all the angles are equal but all the sides are not. The only regular quadrilateral is a square.
In many books, including most school text books, pictures of pentagons and hexagons and other polygons are usually shown regular, but remember a polygon does not have to be regular.

The angles inside a polygon are called the internal angles. In a convex polygon all the internal angles are less than 180°; in a concave polygon at least one of the internal angles is more than 180° (a reflex angle). We normally assume that a polygon is convex unless we are told it is concave.

A stellated regular polygon (from the Latin for star) is a special type of concave polygon. We make a regular polygon stellated by adding identical (congruent) isosceles triangles to the sides. The “spikes” can be of any length.

If we extend the sides of a regular pentagon until they meet we have a pentagram, or pentacle; if we extend the sides of a regular hexagon we have a hexagram, or Star of David. These are special stellated polygons, and are sometimes left as lines, rather than filled with a colour.

A five-pointed star (without the inside pentagon) is often associated with Christmas and many other events, although a pentacle (with the inside pentagon and sometimes a circle round it) is often associated with witchcraft and magic; the Star of David (with the inside hexagon) is associated with Judaism and the State of Israel. We could extend the sides of regular polygons with more than six sides but the shapes formed become closer and closer to the original polygon and are not very interesting.
If we extend one side of a polygon we form the external angle.
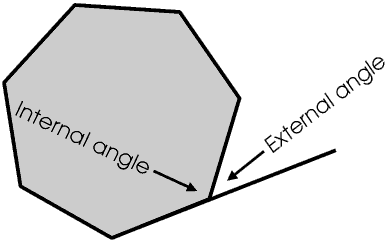
The internal angle and external angle at each vertex of the polygon add up to 180°. If we draw a large polygon on the ground and then walk along one side of it until we reach its end, the external angle is the angle we must turn through in order to be able to walk along the next side. If we walk all round the polygon so that we come back to our starting point and are facing the same way as when we started we shall have turned through a total of 360°. This means that the sum of the external angles of any polygon is always 360°, however many sides it has, and whether it is regular or irregular. In turn, this allows us to work out the sum of the internal angles for any polygon.
We can show that for an n-sided polygon the sum of the internal angles, in degrees, is 180 × (n - 2). This is true for any polygon, it does not have to be regular. For a triangle (n = 3) the sum of the internal angles is 180°, for a quadrilateral it is 360° for a pentagon it is 540° and for a hexagon it is 720°.
If we know all the sides of a triangle we can find all the angles, and this important property leads to a whole branch of mathematics called trigonometry. But this is not true for any other polygon. This is discussed on another Page of my Web Site.Triangles and Quadrilaterals have their own Pages on my Web Site.