If we have three rods and join them at their ends we make a triangle.


There is only one way of joining the rods in this way, that is, in any triangle once we have fixed the length of the sides we have also fixed the size of the angles. This is always true of all triangles, it is never true of any other straight line shape. A whole branch of mathematics, called trigonometry, is based upon this very simple idea.
We call an eight-sided figure an octagon, from the Greek for eight sides. Similarly a hexagon has six sides and a pentagon has five sides. We could call a three-sided shape a trigon, from the Greek for three sides, but we more usually call it a triangle, from the Latin for three corners. But the trigon in trigonometry comes from the Greek, so trigonometry comes from two Greek words and means measuring with triangles. This is much more fully explained in the Page on Trigonometry and the Global Positioning System.
Trigonometry involves the three trigonometric functions of sine (sin), cosine (cos), and tangent (tan), but these functions also have very many uses outside triangles. This Page is mainly about trigonometry and triangles. Here sines and cosines are much more useful than tangents. Tangents come into their own when working with slopes but are not considered further on this Page.
The trigonometric functions are usually first introduced to young people and other students by considering a right-angled triangle.
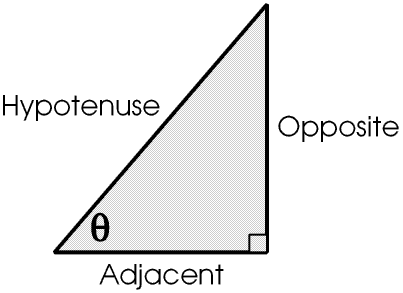
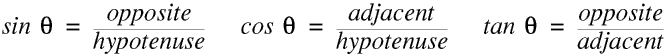
We can see that sin 0 ° and cos 90° are 0, and sin 90° and cos 0° are 1, and for all values of θ between 0° and 90° sin θ and cos θ are between 0 and 1.
This introduction is fine if we are only interested in right-angled triangles, but we need to take a slightly broader view if we want to work with acute- or obtuse-angled triangles, or anything to do with any sort of wave, waves on the sea, light waves, sound waves, radio waves etc.
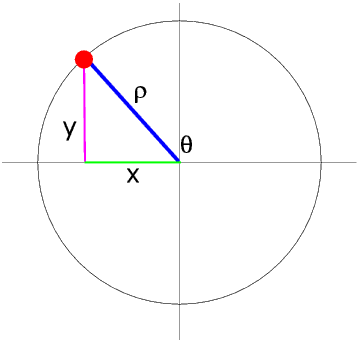
We can give the position of a point in two dimensions in two different ways.
Cartesian co-ordinates are named after the French mathematician René Descartes (1596 - 1650). The position of a point is given by its distance from the two axes (almost invariably called X and Y).
In polar co-ordinates the position of a point is given by its distance from the origin and the angle between the line from the point to the origin and the horizontal line through the origin. The length of the line is always positive and the angles are measured anti-clockwise.When we are plotting graphs in maths and science we usually use Cartesian co-ordinates, but in everyday life we more normally use “distance and direction”, even if we do not necessarily think of them as polar co-ordinates.
We usually use x and y for the position of a point in Cartesian co-ordinates and ρ (the Greek letter rho) and θ for its position in polar co-ordinates.
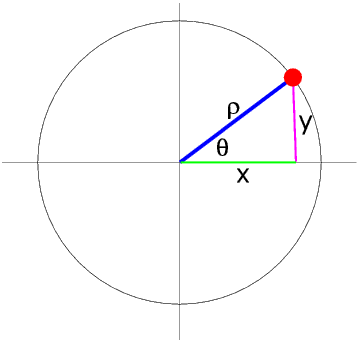
It is important to understand that this is the Rule for all values of θ, not only for values between 0° and 90°.
A circle can be divided into four quadrants. In the First Quadrant (the one shown above) θ is in the range 0° to 90°, and x and y are both positive. So sin θ and cos θ are also both positive. In this Quadrant, but only in this Quadrant, θ and ρ are one of the angles and the hypotenuse in a right angled triangle, hence of course the simplified formulae for sine and cosine given above.
In the Second Quadrant θ is between 90° and 180°.
Here y is positive but x is negative so sin θ is positive but cos θ is negative. We can see that sin θ = sin (180° - θ) and cos θ = - (cos 180° - θ).
What this means is that, if θ is between 0° and 180° (and all the angles inside a triangle must be), for each value of θ there is only one value of sin θ and one value of cos θ, and for each value of cos θ there is only one value of θ, but for each value of sin θ (except sin θ = 1, when θ is 90°) there are two values of θ, one acute and one obtuse - the two values add up to 180° (the two angles are supplementary).On this Page we are concerned only with trigonometry and triangles so we do not need to consider the Third and Fourth Quadrants. But they, and sine waves, and everything which depends upon sine waves, are fully considered in the Page on Polar and Cartesian Co-Ordinates and Circular Motion.
If we are given one side and two other pieces of information about a triangle (for example one other side and one angle) we can find all the other sides and angles by using the Sine and Cosine Rules.